Question
Question: A convex lens forms a real image 4 cm long on the screen. When the lens is shifted to a new position...
A convex lens forms a real image 4 cm long on the screen. When the lens is shifted to a new position without disturbing the object or the screen, again real image is formed on the screen which is 16 cm long. The length of the object is
A) 8 cm.
B) 10 cm.
C) 12 cm.
D) 6 cm.
Solution
Magnification is defined as the enlarged image that any lens or mirror can produce. The enlargement of the image depends on the power of the lens or the mirror the more the power the easily the image will be enlarged.
Formula used:
The formula of the magnification is given by,
m=h1h2
Where m is the magnification h1 is the object height and h2 is the image height.
The formula of the magnification can be also expressed as,
m=−uv
Where m is the magnification v is the image distance and u is the object height.
Complete step by step answer:
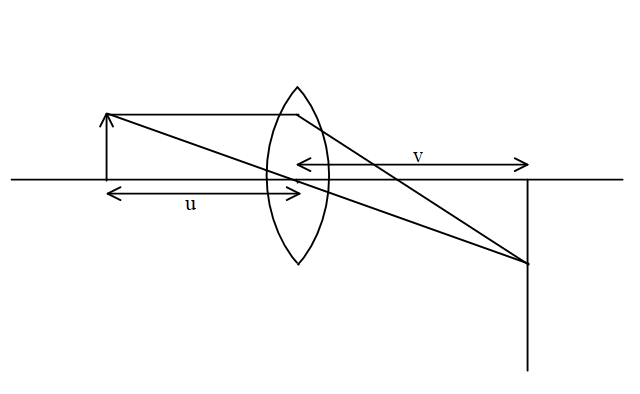
It is given in the problem that a convex lens forms a real image 4 cm on the screen the lens is then shifted to a new position and then the image formed is 16 cm long and we need to find the length of the object.
The formula of the magnification is given by,
m=h1h2
Where m is the magnification h1 is the object height and h2 is the image height.
Also the formula of the magnification in terms of the object and image distance is given by,
m=−uv
Where m is the magnification v is the image distance and u is the object height.
At initial position the magnification is given by,
⇒m1=h1h2=−uv
⇒h14=−uv………eq. (1)
At the new position, let the lens be an object distance v and image distance be u this will also give real image on the screen as the object and the screen both are not disturbed.
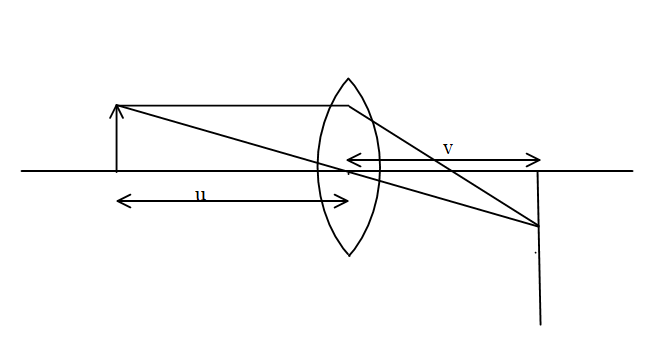
⇒m2=h1h2
⇒m2=h1h2=−vu
On substituting the corresponding values,
⇒h116=−vu………eq. (2)
Multiplying equation (1) and (2) we get,
⇒m=m1×m2
⇒(−uv)×(−vu)=(h14)×(h116)
On substituting the corresponding values,
⇒1=(h14)×(h116)
On simplification,
⇒h12=64
⇒h1=64
On further simplification,
⇒h1=8cm.
The object height is 6 cm. The correct option is option A.
Note:
The image that the lens enlarges depends upon the image and the object distance from the centre of the lens or the mirror. The object and the screen were not disturbed and the lens was shifted to a new position which means that the object and image distance have reversed.
