Question

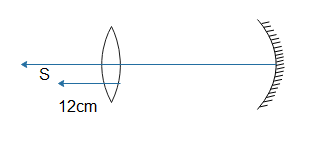
A converging lens of focal length 15cm and a converging mirror of focal length 20cm are placed with their principal axis coinciding. A point source S is placed on the principal axis at a distance of 12cm from the lens as shown in the figure. It is found that the final beam comes out parallel to the principal axis. Find the separation between the mirror and the lens.

Answer 1

We have been provided with the focal length of lens as well as focal length of mirror. Calculate image distance of lens by using lens maker formula. This image will act as a source for mirror use mirror formula to calculate image distance. Hence separation between lens and mirror can be calculated.

Formula used: Formula of lens make is given by
$\dfrac{1}{f}=\dfrac{1}{v}-\dfrac{1}{u}$
Where, f = focal length of lens, v = image distance, u = object distance
Mirror formula is given by
$\dfrac{1}{f}=\dfrac{1}{v}+\dfrac{1}{u}$
Where, f = focal length of mirror, v = image distance, u = object distance.

Complete step by step answer:

As you can see in the figure, we have a converging lens whose focal length is 15cm. We have a converging mirror whose focal length is 20cm. A source S is placed at a distance of 12cm from the lens, as shown in figure. Now we need to find out the separation between lens and mirror.
For lens: Now, let’s find out image distance formed by a lens. Let u be the object distance, f be the focal length of the lens and v be the image distance then according to the lens maker formula.
$\dfrac{1}{f}=\dfrac{1}{v}-\dfrac{1}{u}....(1)$
Focal length (f) = 15cm
Object distance (u)= -12cm
(Consider s is placed at a 12cm from the lens. Therefore u=-12)
Negative signs in formula represent that the object has been placed on the left side of the lens. Put value in equation(1), we get,
$\begin{aligned} & \dfrac{1}{15cm}=\dfrac{1}{v}-\dfrac{-1}{-12cm} \\\ & i.e.\text{ }\dfrac{1}{v}=\dfrac{1}{15}-\dfrac{1}{12} \\\ & v=-60cm.......(2) \\\ \end{aligned}$
This is the image distance formed by a lens. As you can see in the figure, ray emerges from the source (S) incident on the lens. This ray partially reflected and refracted the point where the reflected ray meets the principal axis, an image (${{I}_{1}}$) formed at a distance of 60cm.
Now the ray which is refracted from the lens, reflected back from the mirror and again this reflected ray incident on the lens and as you can see, final beams come out parallel to the principal axis. The image formed by the mirror is ${{I}_{2}}$.
We know that, if ray is passing through a focal point then only parallel ray emerges and since ${{s}^{'}}$ ray is parallel therefore image (${{I}_{2}}$) must be at force point or length of lens. Hence distance between P and ${{I}_{2}}$ must be equal to 15cm.

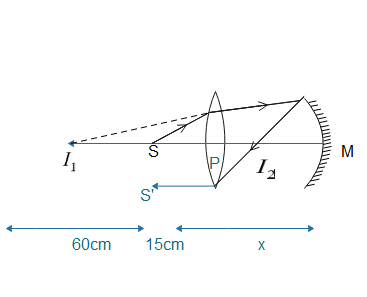
Now, let’s find the distance x if we consider M as the origin of the mirror then ${{I}_{1}}$ must be the source which is acting as a source for the mirror. So object distance must be sum of 60cm, 15cm and x cm i.e.
$\begin{aligned} & u=60+15+x=-(75+x) \\\ & v=-x.......\left( 3 \right) \\\ \end{aligned}$
Focal length of mirror is given in question i.e., 20cm
$\therefore F=-20cm......\left( 4 \right)$
(According to sign convention)
The expression of mirror formula is given as,
$\begin{aligned} & \dfrac{1}{f}=\dfrac{1}{u}+\dfrac{1}{v} \\\ & \Rightarrow \dfrac{1}{-20}=\dfrac{1}{-(75+x)}+\dfrac{1}{-x} \\\ & \Rightarrow \dfrac{1}{20}=\dfrac{1}{75+x}+\dfrac{1}{x} \\\ & \Rightarrow \dfrac{1}{20}=\dfrac{x+75+x}{75x+{{x}^{2}}} \\\ & \Rightarrow 75x+{{x}^{2}}=20\times 2x+1500 \\\ & \Rightarrow {{x}^{2}}+75x-40x-1500=0 \\\ & \Rightarrow {{x}^{2}}+35x-1500=0 \\\ \end{aligned}$
Now let’s find the roots of quadratic equation, we get,
$\begin{aligned} & x=\dfrac{-{{b}^{2}}\pm \sqrt{{{b}^{2}}-4ac}}{2a} \\\ & \Rightarrow x=\dfrac{-{{\left( 35 \right)}^{2}}\pm \sqrt{{{\left( 35 \right)}^{2}}-4\times \left( 35 \right)\left( -1500 \right)}}{2\times 1} \\\ \end{aligned}$
By solving, we get,
$x=25\text{ or x=-60 }$
Distance cannot be negative therefore x = -60 wont possible hence x = 25 is valid distance the separation between the mirror and lens is given by (15+x) as shown in figure. Put value of x, we get
$15+25=40cm$
Therefore, the separation between lens and mirror is 40cm.

Note: Do not forget to use sign convention for image and object distance. Negative sign in equation (3), indicates that image is formed on the left side of the mirror. Also a negative sign from equation (4) indicates that focal length lies on the left side of the mirror. Question has stated that a lens is a converging lens and a converging lens is nothing but a convex lens.