Question

A converging lens (index of refraction $= 1.60$ ) is pictured in five different settings in the upper left, it is in the air where the index of refraction is $1.00$ . In the other four situations the lens is submerged under fluids with labelled indices of refraction. In which situation does the lens have the shortest focal length?

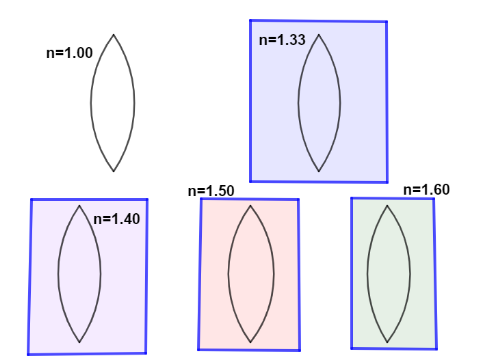
A. When the lens is in air
B. When the lens is in blue fluid
C. When the lens in in purple fluid
D. When the lens in red fluid

Answer 1

In order to solve this question we need to know about convex and concave lenses. Convex lenses are converging lenses, having thicker in the middle than edges, it converges parallel light beam falling on it on a point known as focal point so the image form is real. Concave lenses are diverging lenses having thicker edges then middle, it diverges parallel light beam falling on it such that it appears to come from one point known as focal point so the image formed is virtual.

Complete answer:
To solve the problem we need to understand the relation between refractive index and focal length. So for a lens focal length is inversely proportional to the refractive index which is,
$f = \dfrac{k}{\mu }$
where $k$ is constant.

So less refractive index more the focal length. So in a given problem the refractive index of air is $1.00$ compared with others having high refractive index.
-Blue $1.33$
-Purple $1.40$
-Red $1.50$
-Green $1.60$
So the air has the least refractive index and a large focal length.

So the correct option is A.

Note: It should be remembered that from the Cauchy relation, refractive index is inversely proportional to wavelength so less the refractive index higher the wavelength of light. Also velocity of light in different media is different due to different refractive index so in short refractive index is an important concept as it provides much information on different aspects of nature of lens behaving in different mediums.