Question
Question: A container of width \[2a\] is filled with a liquid. A thin wire of the weight per unit length \[\la...
A container of width 2a is filled with a liquid. A thin wire of the weight per unit length λ is gently placed over the liquid surface in the middle of the surface as shown in the figure. As a result, the liquid surface is depressed by a distance y(y<<a) and determines the surface tension of the liquid.
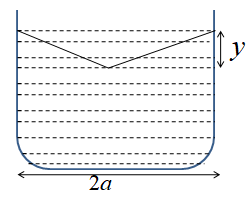
Solution
The surface tension of a liquid is occurred by the attraction of the particles in the surface layer by the bulk of the liquid, which tends to minimize surface area is also defined as the surface tension.The liquid particles together along the surface when the particles are pulled toward the rest of the liquid. The surface tension is the ratio of the surface force to the length along which the force acts. We can determine the surface tension of the liquid by using the given diagram.
Complete step by step answer:
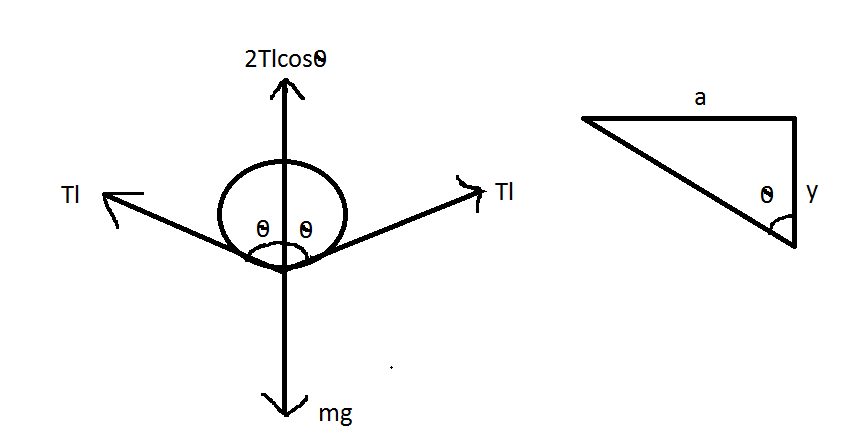
The figure shows that the free body diagram of a wire.
Let l be the length of the wire. If λ is mass per unit length of wire, the weight of wire =(lx)g (acting vertically downward).
Vertical force due to surface tension =2Tlcosθ (upward)
Therefore for vertical equilibrium 2Tlcosθ=(lλ)g
T=2cosθλg
From the figure,
⇒cosθ=yy2+a2=ay (Fory<<a)
⇒T=2(ay)λg=2yλg
Thus, the correct answer of the surface tension of the liquid is T=2yλg.
Note:
The attractive forces between the particles in the given liquid but also on the forces of attraction of solid, liquid, or gas in contact with it do not only depend upon the surface tension.
The energy responsible for the phenomenon of surface tension may be almost equal to the equivalent of the work or energy required to remove the surface layer of molecules in a unit area.
