Question

A container in the shape of a right circular cylinder is $\dfrac{1}{2}$ full of water. If the volume of water in the container is $36$ cubic inches and the height of the container is $9$ inches, what is the diameter of the base of the cylinder, in inches?
A. $\dfrac{{16}}{{9\pi }}$
B. $\dfrac{4}{{\sqrt \pi }}$
C. $\dfrac{12}{{\sqrt \pi }}$
D. $4\sqrt {\dfrac{2}{\pi }}$

Answer 1

In this problem it is given that a container in the shape of a right circular cylinder is half full of water. If the volume of water in the container is $36$ cubic inches and the height of the container is $9$ inches then we have to find the diameter of the cylinder. Firstly, we use the right circular cylinder volume formula and find the radius of the cylinder. Then find the diameter of the cylinder.

Complete step by step solution
It is given that a right circular cylinder is $\dfrac{1}{2}$ full of water, volume of water in the container is $36$ cubic inches and the height of the container is $9$ inches.
We have to find the diameter of the base of the cylinder in inches.

Let us first draw the diagram of the right circular cylinder:

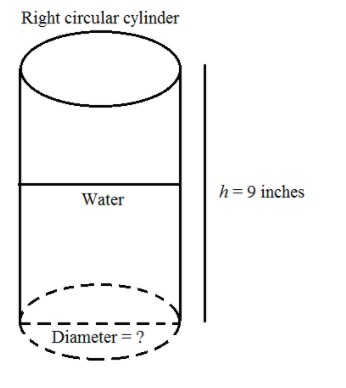
Let,
$r$ be the radius of the cylinder.
Since the container of a right circular cylinder is $\dfrac{1}{2}$ full of water and height of the container is $9$ inches then height of the water is $= 9\left( {\dfrac{1}{2}} \right) = 4.5$
Now, use the formula of volume of the right circular cylinder.
Volume of the cylinder$= \pi {r^2}\left( {height} \right)$
Substitute $36$ for volume and $4.5$ for height in above equation.
$\Rightarrow 36 = \pi {r^2}\left( {4.5} \right)$
Divide each side by $4.5$
$\begin{array}{l} \Rightarrow 8 = \pi {r^2}\\\\\end{array}$
Divide each side by $\pi$
$\Rightarrow \dfrac{8}{\pi } = {r^2}$
Take the square root on each side.
$\begin{array}{l} \Rightarrow \sqrt {\dfrac{8}{\pi } = } \sqrt {{r^2}} \\\ \Rightarrow \sqrt {\dfrac{8}{\pi }} = r\end{array}$
Simplify further.
$\Rightarrow r = 2\sqrt {\dfrac{2}{\pi }}$
Therefore, the radius of the cylinder is $r = 2\sqrt {\dfrac{2}{\pi }}$ inches.
Since, the diameter is twice the length of the radius.
Thus, the diameter of the base of the cylinder$= 2r = 2\left( {2\sqrt {\dfrac{2}{\pi }} } \right) = 4\sqrt {\dfrac{2}{\pi }}$ inches.
Hence the correct answer is D.

Note: Here given a right circular cylinder is half full of water with volume of water in the container is $36$ cubic inches and the height of the container is $9$ inches then we have to find the diameter of the cylinder. Firstly, we find the radius of the cylinder with the help of formula of volume of the cylinder and then finally we get the diameter of the cylinder.