Question
Question: A consistent force \(F = {m_1}g/2\) is applied on the block of mass \({m_2}\) as shown in figure. Th...
A consistent force F=m1g/2 is applied on the block of mass m2 as shown in figure. The string and the pulley are light and the surface of the table is smooth. Find the acceleration of m2.
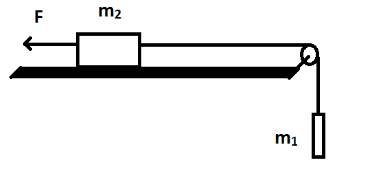
Solution
To solve this problem, we need to use two main concepts. First is the tensile force and second is Newton's second law of motion. We will consider the horizontal forces acting on mass m2 and vertical forces on the mass m1. By this we can obtain two equations which will help us find the value of the acceleration of m2.
Complete step by step answer:
Let us consider the forces on the system as shown in figure. Let T be the tension in the rope.
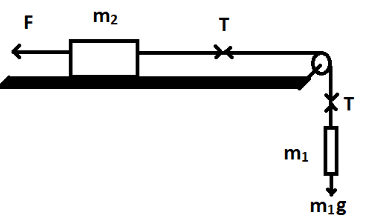
Now, we will consider the horizontal forces action on mass m2.
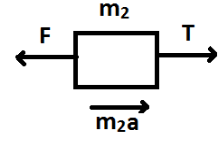
As shown in the figure, two forces are clearly visible action in the opposite direction on mass m2. First is force F and second is the tensile force T. Moreover. If we take acceleration as a, then according to Newton’s second law of motion, there is another force m2aacting in the right direction.
Equating these horizontal forces, we get
F=m2a+T
It is given that F=m1g/2
\dfrac{{{m_1}g}}{2} = {m_2}a + T \\\
\Rightarrow T = \dfrac{{{m_1}g}}{2} - {m_2}a \\\
Now, we will consider vertical forces acting on mass m1.
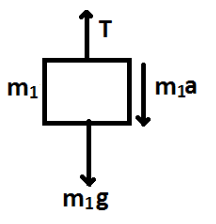
Here, tensile force is acting upwards and weight and force due to motion acts downwards.
Equating the vertical forces, we get
T=m1a+m1g
Putting T=2m1g−m2a in this equation, we get
2m1g−m2a=m1a+m1g ⇒m1a+m2a=2m1g−m1g ⇒a(m1+m2)=−2m1g ∴a=−2(m1+m2)m1g
Thus the acceleration of m2is −2(m1+m2)m1g.
Note: Here, we have used Newton’s second law of motion to determine the answer of this question. This law states that the acceleration of an object is directly related to the net force and inversely related to its mass. Thus, when a force is applied on the body and if its mass is known, then the acceleration can be determined by applying this law.
