Question

A conical tank (with vertex down) is $10$ feet across the top and $12$ feet deep. Water is flowing into the tank at a rate of $5$ cubic feet per minute. Find the rate of change of the depth of the water when the water is $4$ feet deep.

Answer 1

In this question,we need to find the rate of change of the depth of the water when the water is $4$ feet deep. Given that the radius of the tank is $10$ feet. From this, we can find the radius of the tank. Also the height of the tank is $12$ feet and the water is $8$ feet deep. The rate of change of the depth of the water can be found by differentiating the volume of the cone. The differentiation is nothing but a rate of change of function with respect to an independent variable given in the function. First let us consider the radius of the tank to be $r$ and $h$ be the height of the tank . We need to substitute the value of $r$ in the volume formula. Then on differentiating we can find the rate of change of the depth of the water when the water is $4$ feet deep.

Formula used:
The volume of the cone ,
$V = \dfrac{1}{3}\ \pi r^{2}\ h$
Where $r$ is the radius of the cone and $h$ is the height of the cone.
Derivative rule used :
$\dfrac{d}{dx}x^{n} = nx^{n – 1}$

Complete step-by-step answer:

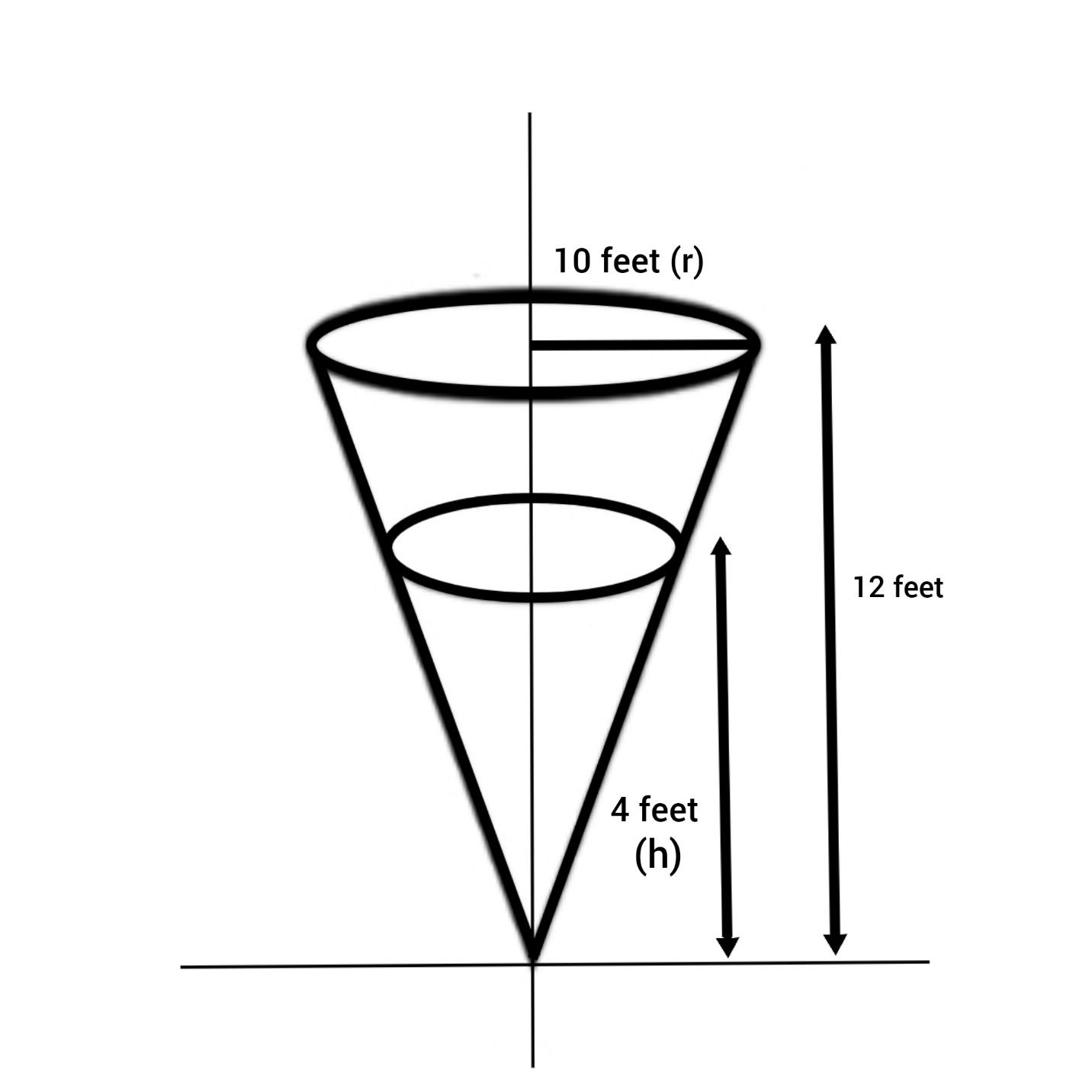
Let us consider the radius of the tank to be $r$ and $h$ be the height of the tank .
Given, the conical tank is $10$ feet across and $12$ feet deep, that is the radius of the tank is $10$ feet and height is $12$ feet.
$r = 10$
By relating the radius $r$ to the height $h$ ,
$\Rightarrow \dfrac{r}{h} = \dfrac{10}{12}$
Thus $r = \dfrac{5}{6}h$
We know volume of the cone is $\dfrac{1}{3}\pi r^{2}h$
$V = \dfrac{1}{3}\pi r^{2}h$
By substituting $r = \dfrac{5}{6}h$
We get,
$V = \dfrac{1}{3}\pi{(\dfrac{5}{6}h)}^{2}h$
On simplifying,
We get,
$V = \dfrac{25}{108}\pi h^{3}$
On differentiating $V$ with respect to time $t$ ,
We get,
$\dfrac{dV}{dt} = \dfrac{25}{108}\pi\left( 3h^{2}\dfrac{dh}{dt} \right)$
Also given the rate change of volume is $5$ cubic feet per minute.
By substituting the value of volume rate,
We get,
$5 = \dfrac{25}{108}\pi\left( 3h^{2}\dfrac{dh}{dt} \right)$
We need to find the rate of change of the depth of the water when the water is $4$ feet deep,
By substituting the value of $h = 4$ and $\pi = 3.14$ ,
We get,
$5 = \dfrac{25}{108}\left( 3.14 \right)\left( 3\left( 4 \right)^{2}\dfrac{dh}{dt} \right)$
On simplifying,
We get,
$5 = 0.719\left( (48)\dfrac{dh}{dx} \right)$
On multiplying the term inside,
We get,
$5 = 34.5\dfrac{dh}{dt}$
By rewriting the terms,
We get,
$\dfrac{dh}{dx} = \dfrac{5}{34.5}$
On simplifying,
We get $\dfrac{dh}{dt} \approx 0.146$ feet/min
Thus we get the rate of change of the depth of the water is approximately $0.146$ feet/min.
Final answer :
The rate of change of the depth of the water is approximately $0.146$ feet/min.

Note: Mathematically , Derivative helps in solving the problems in calculus and in differential equations. The derivative of $y$ with respect to $x$ is represented as $\dfrac{dy}{dx}$ . Here the notation $\dfrac{dy}{dx}$ is known as Leibniz's notation . In derivation, there are two types of derivative namely first order derivative and second order derivative. A simple example for a derivative is the derivative of $x^{3}$ is $3x$ . Derivative is applicable in trigonometric functions also .