Question

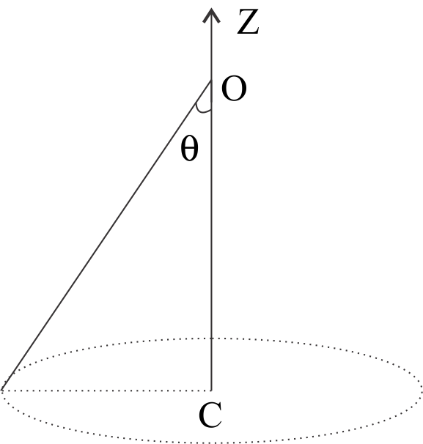
A conical pendulum of length $1m$ makes an angle $\theta = 45^\circ$ w.r.t Z−axis and moves in a circle in the $XY$ plane. The radius of the circle is $0.4m$ and its centre is vertically below $O$. The speed of the pendulum, in its circular path, will be: ${\text{(Take g = 9}}{\text{.8m}}{{\text{s}}^{ - 2}})$

(A) $0.4{\text{m/s}}$
(B) $4{\text{m/s}}$
(C) $0.2{\text{m/s}}$
(D) $2{\text{m/s}}$

Answer 1

Hint A conical pendulum moves in a circular path whose radius is given. The angle in which the conical pendulum makes with the circle is provided. We have to find the speed of the pendulum, for this we should have known the concept of conical pendulum.

Complete step by step answer
A conical pendulum consists of a mass on the end of a string suspended from a point which moves in a circular path.
Let us consider a conical pendulum having the mass $m$ revolving in a circle at a constant velocity $v$ on a string of length $l$ at an angle of $\theta$.
There will be two forces acting on the mass,
Tension and centripetal force.
The Tension exerted can be resolved into a horizontal component, $Tsin\left( \theta \right)$ and vertical component $Tcos\left( \theta \right)$.
The horizontal component of the tension experience centripetal force since the conical pendulum travels in a circular path of radius r with a constant velocity v
$T\sin \theta = \dfrac{{m{v^2}}}{r}$
We can rearrange the above equation as
$T = \dfrac{{m{v^2}}}{{r\sin \theta }}{\text{ }} \to {\text{1}}$
Since there is no acceleration in the vertical direction, the vertical component is equal and opposite to the weight of the mass so, the vertical component of tension is
$T\cos \theta = mg$
We can rearrange the above equation as
$T = \dfrac{{mg}}{{\cos \theta }}{\text{ }} \to 2$
Equating 1 and 2
$\Rightarrow \dfrac{{m{v^2}}}{{r\sin \theta }} = \dfrac{{mg}}{{\cos \theta }}$
$\Rightarrow {v^2} = \dfrac{{gr\sin \theta }}{{\cos \theta }}$
$\Rightarrow {v^2} = gr\tan \theta {\text{ }} \to 3$
Given that,
The radius of the circular path, $r = 0.4m$
The conical pendulum makes an angle $\theta = 45^\circ$
The acceleration due to gravity, $g = 9.8{\text{m/s}}$
Substitute these given values in the equation 3
$\Rightarrow {v^2} = gr\tan \theta$
$\Rightarrow {v^2} = 9.8 \times 0.4 \times \tan 45^\circ$
$\Rightarrow {v^2} = 9.8 \times 0.4 \times 1$
$\Rightarrow {v^2} = 3.9 = 4{\text{m/s}}$
$\Rightarrow v = \sqrt 4 {\text{m/s}}$
$\Rightarrow v = 2{\text{m/s}}$
The speed of the pendulum is $2{\text{m/s}}$

Hence the correct answer is option D) $2{\text{m/s}}$

Note A conical pendulum is similar to an ordinary simple pendulum, instead of swinging back and forth, the mass of a conical pendulum moves in a circle with the string tracing out a cone.