Question

A conical flask of base radius r and height h is full of milk. The milk is now poured into a cylindrical flask of radius 2r. What is the height to which the milk will rise in the flask?
(a) $\dfrac{h}{3}$
(b) $\dfrac{h}{6}$
(c) $\dfrac{h}{9}$
(d) $\dfrac{h}{12}$

Answer 1

In this question, we first need to find the volume of the conical flask with the given dimensions which is given by the formula $\dfrac{1}{3}\pi {{r}^{2}}h$. Now, we need to find the volume of the cylindrical flask with the given dimensions which is given by the formula $\pi {{r}^{2}}h$. Then equate both the volumes to get the height of the cylindrical flask which gives the result.

Complete step by step answer:
RIGHT CIRCULAR CONE:
A right circular cone is a solid generated by revolving of a right angled triangle through one of its sides containing the right angle as axis.
Volume of a cone is given by the formula
$\dfrac{1}{3}\pi {{r}^{2}}h$
RIGHT CIRCULAR CYLINDER:
A right circular cylinder is considered as a solid generated by the revolution of a rectangle about one of its sides
Volume of the cylinder is given by the formula
$\pi {{r}^{2}}h$
Let us assume that the volume of conical flask as v and that of cylindrical flask as V

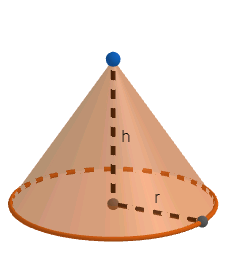
Now, the volume of the milk in the conical flask with radius r and height h is given by
$\Rightarrow v=\dfrac{1}{3}\pi {{r}^{2}}h$
Now, let us assume that the height of the cylindrical flask as H and its radius as R
Now, form the formula of volume of a cylinder we have
$V=\pi {{R}^{2}}H$
Here, given in the question that
$R=2r$

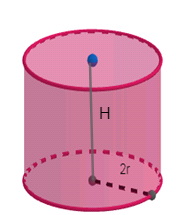
Now, on substituting the respective values in the above formula we get,
$\Rightarrow V=\pi {{\left( 2r \right)}^{2}}H$
Now, this can be further written as
$\therefore V=4\pi {{r}^{2}}H$
Here, as milk is being poured from conical flask into cylindrical flask we have
$\Rightarrow v=V$
Now, on substituting the respective values we get,
$\Rightarrow \dfrac{1}{3}\pi {{r}^{2}}h=4\pi {{r}^{2}}H$
Now, on cancelling out the common terms on both the sides we have
$\Rightarrow \dfrac{1}{3}h=4H$
Now, on further rearranging the terms we get,
$\therefore H=\dfrac{h}{12}$
Hence, the correct option is (d).

Note: Instead of finding the volumes of the conical flask and cylindrical flasks and then equating then we can also find it by finding what becomes to the height if we double the radius. Because we know that the volume of the cylinder is thrice the volume of the cone which gives the result.
It is important to note that when we pour the milk in the conical flask into the cylindrical flask the volume remains the same but not the area. If we equate the areas instead of volumes then the result will be incorrect.