Question

A cone whose height is equal to the diameter, is increasing in volume at the rate of $40c{{m}^{3}}/s$ . At what rate is the radius increasing when its circular base area is $1{{m}^{2}}$ ?
(A) $1mm/s$
(B) $0.001cm/s$
(C) $2mm/s$
(D) $0.002cm/s$

Answer 1

We know that the formulae for finding the volume of the cone given as $V=\dfrac{1}{3}\pi {{r}^{2}}h$ . As given the height of the cone is equal to its diameter which is mathematically given as $h = 2r$. Now we will substitute this in the formulae of volume. Now we will differentiate the terms of both sides. We already know the rate of volume and the value of radius. Based on these values, we can find the rate of increase in radius.

Complete step-by-step solution:
Now considering from the question we have been asked to find the increasing rate of radius using the given information in the question which is stated as follows “A cone, whose height is equal to the diameter, is increasing in volume at the rate of $40c{{m}^{3}}/s$ and its circular base area is $1{{m}^{2}}$”.
From the basic concepts we know that the formula for finding the volume of the cone given as $V=\dfrac{1}{3}\pi {{r}^{2}}h$ .
As given the height of the cone is equal to its diameter which is mathematically given as $h=2r$ .

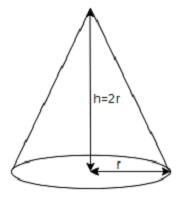
Now we will substitute this value in the formulae then we will have
$\begin{aligned} & \Rightarrow V=\dfrac{1}{3}\pi {{r}^{2}}\left( 2r \right) \\\ & \Rightarrow V=\dfrac{2}{3}\pi {{r}^{3}} \\\ \end{aligned}$
Now we will differentiate this expression as we need to find the rate at which the radius is increasing for that we will use the formulae given as $\dfrac{d}{dx}{{x}^{n}}=n{{x}^{n-1}}$ after that we will have
$\begin{aligned} & \Rightarrow \dfrac{d}{dt}V=\dfrac{2}{3}\pi \left( \dfrac{d}{dt}{{r}^{3}} \right) \\\ & \Rightarrow \dfrac{d}{dt}V=\dfrac{2}{3}\pi \left( 3{{r}^{2}} \right)\dfrac{dr}{dt} \\\ & \Rightarrow \dfrac{d}{dt}V=2\pi {{r}^{2}}\dfrac{dr}{dt} \\\ \end{aligned}$
In the question it is given that the volume of the cone is increasing at the rate of $40c{{m}^{3}}/s$ .
By using this we will have
$\begin{aligned} & \Rightarrow 40c{{m}^{3}}/s=2\pi {{r}^{2}}\left( \dfrac{dr}{dt} \right) \\\ & \Rightarrow \dfrac{40}{{{10}^{6}}}{{m}^{3}}/s=2\pi {{r}^{2}}\left( \dfrac{dr}{dt} \right) \\\ & \Rightarrow 4\times {{10}^{-5}}{{m}^{3}}/s=2\pi {{r}^{2}}\left( \dfrac{dr}{dt} \right) \\\ \end{aligned}$ .
The area of the circular base is given as $1{{m}^{2}}$ that implies that $\pi {{r}^{2}}=1{{m}^{2}}$
By substituting this value we will have
$\begin{aligned} & \Rightarrow 4\times {{10}^{-5}}{{m}^{3}}/s=2\left( 1{{m}^{2}} \right)\dfrac{dr}{dt} \\\ & \Rightarrow 2\times {{10}^{-5}}m/s=\dfrac{dr}{dt} \\\ \end{aligned}$
As we know that $100cm=1m$ by using this we will have
$\begin{aligned} & \Rightarrow \dfrac{dr}{dt}=2\times {{10}^{-5}}\times {{10}^{2}}cm/s \\\ & \Rightarrow \dfrac{dr}{dt}=2\times {{10}^{-3}}cm/s \\\ & \Rightarrow \dfrac{dr}{dt}=0.002cm/s \\\ \end{aligned}$
Therefore we can conclude that for a cone whose height is equal to the diameter, is increasing in volume at the rate of $40c{{m}^{3}}/s$ and when its circular base area is $1{{m}^{2}}$ then the rate at which the radius increasing will be $0.002cm/s$ . Hence option D is correct.

Note: While answering questions of this type we should be sure with the calculations and concepts that we apply while answering. The unit conversions should be done carefully. If we had not made the unit conversions then we will have the answer completely vary from the answer. We should also not make mistakes in taking the diameter = two times the radius if we take wrong our whole solution will be wrong.