Question
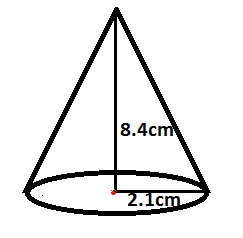
Question: A cone is \(8.4cm\) high and the radius of its base is \(2.1cm\). It is melted and recast into a sph...
A cone is 8.4cm high and the radius of its base is 2.1cm. It is melted and recast into a sphere. The radius of the sphere is
A.4.2cm
B.2.1cm
C.2.4cm
D.1.6cm
Solution
First, we shall analyze the given information. We are given a cone whose radius is 2.1cm and height is 8.4cm. The given cone is melted and recast into a sphere. We are asked to calculate the radius of the sphere.
If the cone is melted and recast into the sphere, then the volume of the cone will be equal to the volume of the sphere. Using this condition, we can easily find the radius of the sphere.
Formula to be used:
The formula to calculate the volume of a cone is as follows.
The volume of a cone =31πr2h
Where r is the radius of the cone.
The formula to calculate the volume of a sphere is as follows.
The volume of a sphere
Where R is the radius of the cone.
Complete step by step answer:
Let r be the radius of the cone and h be the height of the cone.
It is given that the radius of the cone is r=2.1cm and the height of the cone is h=8.4cm.
The formula to calculate the volume of a cone is as follows.
The volume of a cone =31πr2h
=31π(2.1)2×8.4 ……..(1)
Let R be the radius of the sphere.
The formula to calculate the volume of a sphere is as follows.
The volume of a sphere ……..(2)
It is given that the cone is melted and recast into the sphere. So, the volume of the cone is equal to the volume of the sphere.
Hence, equating (1) and (2), we get
Taking cube roots on both sides, we have
⇒R=2.1cm
Hence, the radius of the sphere is2.1cm
Hence, option B is correct.
Note:
We are given a clue that the given cone is melted and recast into the sphere.
If the cone is melted and recast into the sphere, then the volume of the cone will be equal to the volume of the sphere. Using this condition, we can easily find the radius of the sphere.
