Solveeit Logo
Login

Question

Question: A cone has a perpendicular height of \[12{\text{ cm}}\] and slant height of \[13{\text{ cm}}\]. Calc...

A cone has a perpendicular height of 12 cm12{\text{ cm}} and slant height of 13 cm13{\text{ cm}}. Calculate its total surface area.

Explanation

Solution

We will use some geometrical concepts of 3-Dimensional figures and illustrate them and solve this problem. We will use some formulas like C.S.A=πrlC.S.A = \pi rl and the area of a circle is πr2\pi {r^2}. We will also make use of Pythagoras theorem to solve this problem.

Complete answer:
Generally, a cone is a kind of pyramid with a circular base. It is a 3-Dimensional object. The length from the tip of the cone to the centre of the circle is called the height of the cone. And the length from tip of cone to any point on circumference of the circle is called slant height of cone.

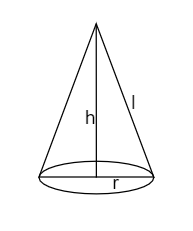
When you observe, the height of the cone is perpendicular to the base, which means the height is perpendicular to radius.
So, height, radius and slant height form a right-angled triangle, where height and radius are perpendicular.

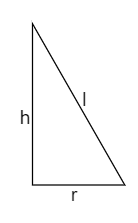
From Pythagoras theorem, we can write it as, h2+r2=l2{h^2} + {r^2} = {l^2} -----(1)
And now, the total surface area of a cone is equal to the sum of curved surface area and the base area.
⇒T.S.A=C.S.A+πr2\Rightarrow T.S.A = C.S.A + \pi {r^2} (As area of a circle is πr2\pi {r^2} )
Now, the curved surface area of a cone is equal to πrl\pi rl where rr is radius and ll is slant height.
⇒T.S.A=πrl+πr2\Rightarrow T.S.A = \pi rl + \pi {r^2}
⇒T.S.A=πr(l+r)\Rightarrow T.S.A = \pi r\left( {l + r} \right)
And from equation (1), h2+r2=l2{h^2} + {r^2} = {l^2}
⇒r2=l2−h2\Rightarrow {r^2} = {l^2} - {h^2}
⇒r=l2−h2\Rightarrow r = \sqrt {{l^2} - {h^2}}
Now, on substituting the values l=13 cml = 13{\text{ cm}} and h=12 cmh = 12{\text{ cm}} in the above equation, we get,
⇒r=(13)2−(12)2=169−144\Rightarrow r = \sqrt {{{(13)}^2} - {{(12)}^2}} = \sqrt {169 - 144}
⇒r=25=5 cm\Rightarrow r = \sqrt {25} = 5{\text{ cm}}
Now, we will finally get the resultant as,
T.S.A=π(5)(13+5)T.S.A = \pi (5)\left( {13 + 5} \right)
⇒T.S.A=(3.142)(5)(18)\Rightarrow T.S.A = (3.142)(5)\left( {18} \right)
So, total surface area of this cone is equal to T.S.A=282.78 cm2T.S.A = 282.78{\text{ c}}{{\text{m}}^2}

Note:
Always remember to mention units after calculating the required. Area is always measured in square units{\text{square units}}. And in the same way, volume is measured in cubic units{\text{cubic units}}. And remember the formula of curved surface area is equal to C.S.A=πrlC.S.A = \pi rl