Question

A conductor with rectangular cross section has dimensions $\left( {4a \times 2a \times a} \right)$ as shown in figure. Resistance across $AB$ is $x$, across $CD$ is $y$ and across $EF$ is $Z$.

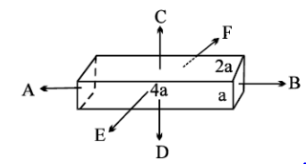
(A) $x = y = z$
(B) $x > y > z$
(C) $y > x > z$
(D) $x > z > y$

Answer 1

Useful formula: Use the relation between the resistance and resistivity to calculate the value of resistance at the point $x,\,y$ and $z$. Substitute the values of length and cross sectional area given in the formula. Compare the values of obtained resistance of $x,\,y$ and $z$to find the answer for this question.

Formulae Used:
Resistance formula is
$R = \dfrac{{\rho l}}{A}$
Where $R$ is the resistance of the conductor, $\rho$ is the resistivity of the conductor, $l$ is the length of the conductor and $A$ is the cross sectional area of the conductor.

Complete step-by-step solution:
The given data from the question are
Resistance across $AB$ is $x$
Resistance across $CD$ is $y$
Resistance across $EF$ is $z$
By using the resistance formula,
The resistance across $x$ is $R = \dfrac{{\rho l}}{A}$. Cross sectional area at $x$ is $4a \times a$.
Substituting the values at the above equation
$x = \dfrac{{\rho \left( {4a} \right)}}{{2a \times a}}$
$x = \dfrac{{\rho \left( {2a} \right)}}{{{a^2}}}$
By simplifying the above equation,
$x = \dfrac{{2\rho }}{a}$
Cross sectional area at $y$ is $4a \times 2a$.
Similarly, finding the values of resistance at $y$.
$y = \dfrac{\rho }{{8a}}$
Cross sectional area at $z$ is $4a \times a$.
In the same way, finding the values of resistance at $z$.
$z = \dfrac{\rho }{{2a}}$
From the obtained values of $x,\,y$ and $z$, it is known that $x > z > y$.
Thus the option (D) is correct.

Note:- Remember that the cross sectional area at a particular point is calculated by the sectional area which is obtained by a sliced section of the considered object. For example: the cross sectional area at $x$ is calculated as the area of the cross section of AB which is $2a \times a$.