Question

A conductor (shown in the figure) carrying constant current I is kept in the x-y plane in a uniform magnetic field B. If F is the magnitude of the total magnetic force acting on the conductor, then the correct statement(s) is (are)

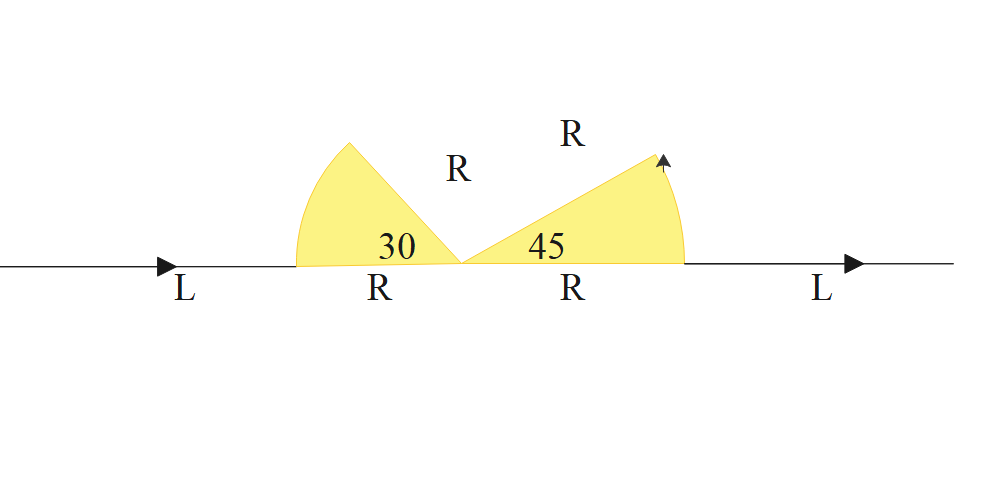
A) if B is along z-axis, $F\alpha (L+R)$
B) if B is along x-axis, F=0
C) if B is along y-axis, $F\alpha (L+R)$
D) id B is along z-axis, F=0

Answer 1

Find the force acting through the conductor as shown in the figure. As the conductor is not informed, find the length of any small element dl, the force acting over the small element dl will be the cross product of the current, length and the magnetic field, verifying the options, we will get the correct options.

Formula used:
$F=il\times B$

Complete step-by-step answer:
As the conductor given is not uniform and the direction of flow of current is different for different parts of the conductor,
Let us assume a small part of the element dl where,
$dl=2(L+R)\hat{x}$
The vector sum of all current elements in wires not parallel to the x axis will lead to resultant current element of length R and current along x axis.
Now, the net force acting on the conductor due to the magnetic field will be,
$\begin{aligned} & F=il\times B \\\ & \Rightarrow F=i(2(L+R)\hat{x})\times B \\\ \end{aligned}$
Now, let’s verify the options,
In option a, if the magnetic field B is along the z-axis, the force acting will be along negative y-direction and is proportional to the length (L+R). Hence, option a is correct.
In option b, if magnetic field B is along x-direction, the force acting on the conductor will be zero as the vector cross product will be zero. Hence, option b is correct.
In option c, if the magnetic field is along the y-direction, the force acting on the conductor will be along the z-axis and will be proportional (L+R). Hence, option c is also correct.
Finally, if magnetic field B is along z-direction, the force acting on the conductor will be along negative y-direction but it will not be equal to zero. Hence, option d is wrong.

So, the correct answers are “Option A,B and C”.

Note: The force acting on any conductor in a magnetic field is a vector and cross product is used in the vector formula. As a cross product of two same directions is zero as the angle between them will be zero, the force will be zero if the current and the magnetic field are in the same direction.