Question

A conductor of uniform resistance (per unit length) bent in the form of an equilateral triangle of side $a$ . It is enclosing an inward magnetic field \vec B = {B_0}{\cos ^2}\omega t\left( { - \overset{\lower0.5em\hbox{ \smash{\scriptscriptstyle\frown} }}{k} } \right) . Then:

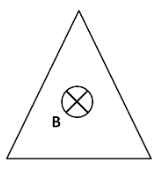
(A) During $0 < t < \dfrac{\pi }{{2\omega }}$ a clockwise current is induced in the coil.
(B) During $0 < t < \dfrac{\pi }{\omega }$ an anticlockwise current is induced in the coil.
(C) During $\dfrac{\pi }{{2\omega }} < t < \dfrac{\pi }{\omega }$ an anticlockwise current flows through it.
(D) During $\dfrac{\pi }{\omega } < t < \dfrac{{3\pi }}{{2\omega }}$ a clockwise current flows through it.

Answer 1

Hint : To answer this question, we need to observe the direction of change of the magnetic flux through the coil for different time intervals. Then, applying Lenz's law we can predict the direction of the current induced in the coil.

Complete step by step answer
The magnetic field is given as \vec B = {B_0}{\cos ^2}\omega t\left( { - \overset{\lower0.5em\hbox{ \smash{\scriptscriptstyle\frown} }}{k} } \right)
We know that ${\cos ^2}{{\theta }} = \dfrac{{1 + \cos 2{{\theta }}}}{2}$ . So we have
\Rightarrow \vec B = {B_0}\left( {\dfrac{{1 + \cos 2\omega t}}{2}} \right)\left( { - \overset{\lower0.5em\hbox{ \smash{\scriptscriptstyle\frown} }}{k} } \right)
For $0 < t < \dfrac{\pi }{{2\omega }}$
For this interval, we have $\cos 2\omega t$ decreasing from $1$ to $- 1$ . So the magnetic field decreases in this time interval, which is into the plane of the paper. Since, the magnetic field is decreasing into the plane of paper, so the magnetic flux decreases through the coil. So according to Lenz's law the direction of the current induced in the coil will be such that the magnetic field due to the coil is into the plane of the paper. From the right hand rule, we get the direction of current to be clockwise.
Hence, option A is correct.
For $\dfrac{\pi }{{2\omega }} < t < \dfrac{\pi }{\omega }$
For this interval, we have $\cos 2\omega t$ increasing from $- 1$ to $1$ . So, this means that the magnetic field is increasing into the plane of the paper. This means that the magnetic flux is increasing into the plane of paper. Therefore, according to Lenz's law, the direction of current induced in the coil will be such that the magnetic field produced is outside the plane of paper. From the right hand rule, we get the direction of the current as anticlockwise. So, an anticlockwise current flows through it.
Hence, option C is correct.
For $0 < t < \dfrac{\pi }{\omega }$
This interval is divided into two sub-intervals, one is $0 < t < \dfrac{\pi }{{2\omega }}$ and the other is $\dfrac{\pi }{{2\omega }} < t < \dfrac{\pi }{\omega }$ . As we have seen above that for the first interval, clockwise current flows through the coil, while for the second interval, an anticlockwise current flows through it. So, the direction of current is not fixed for this whole interval.
Hence, option B is incorrect.
For $\dfrac{\pi }{\omega } < t < \dfrac{{3\pi }}{{2\omega }}$
For this interval, $\cos 2\omega t$ decreases from $1$ to $- 1$ . So, the magnetic field is decreasing into the plane of the paper. This means that the magnetic flux through the loop is decreasing in this interval into the plane of the paper. Therefore according to Lenz's law the direction of the current induced in the coil will be such that the magnetic field due to it is inside the plane of the paper. From the right hand rule, we get the direction of current to be clockwise. So, a clockwise current flows through the loop for this time interval.
Hence, option D is correct.
Therefore, the correct answers are options A, C and D.

Note
We can solve the question also by drawing the graph of ${\cos ^2}\omega t$ . From the graph, we will be able to predict the direction of the change of the magnetic flux through the coil without any calculations. This method is relatively very easy and at the same time very quick.