Question

A conductor is made of an isotropic material (resistivity$\rho$) has rectangular cross-section. The horizontal dimensions of the conductor decrease linearly from $2x$ at one end to $x$ on the other end and vertical dimensions increase from $y$ to $2y$ as shown in the figure. The length of the conductor along the axis is equal to $l$ and a battery is connected across the conductor, then

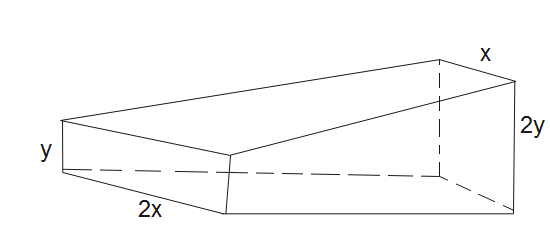
(A). Resistance of the conductor is equal to $\dfrac{4\rho l}{9xy}$
(B). Resistance of the conductor is equal to $\dfrac{9\rho l}{4xy}$
(C). Drift velocity of the conduction electrons is maximum in the middle section
(D). Drift velocity of the conduction electrons is minimum in the middle section

Answer 1

The conductor given in the above figure has a variable area. So the area through which the charge passes changes continuously. The length along x-axis decreases along z-axis and the length along y-axis increases with increase in z-axis, so a direct relation exists between them. Drift velocity is average velocity of electrons; it depends on current, charge density, magnitude of charge and area of cross section.

Formula used:
$A=x'y'$
${{v}_{d}}=\dfrac{I}{NAQ}$

Complete step-by-step solution:
Given that the dimensions along x-axis decrease linearly with z-axis and the dimensions along the y-axis increase linearly with z-axis.

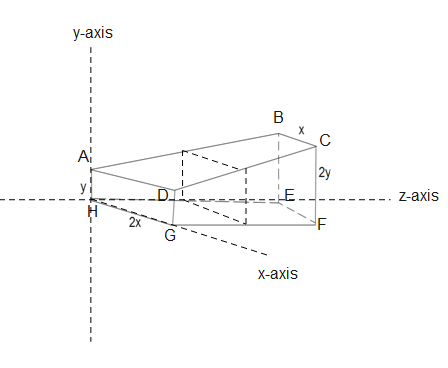
The area of an arbitrary face in the figure through which the charge passes will be-
$\begin{aligned} & A=x'y' \\\ & \Rightarrow A=(2x-xz)(y+yz) \\\ & \Rightarrow A=xy(2-z)(1+z) \\\ \end{aligned}$

We differentiate the above equation with respect to z and equate it to zero to get,
$\begin{aligned} & xy(-1)(1+z)+xy(2-z)(1)=0 \\\ & \Rightarrow -1-z+2-z=0 \\\ & \Rightarrow 2z=1 \\\ & \therefore z=0.5 \\\ \end{aligned}$
Therefore, the area will be maximum at $z=0.5$.

The average velocity of charges flowing through a conductor due to the presence of an electric field is known as drift velocity. It is given by-
${{v}_{d}}=\dfrac{I}{NAQ}$
Here,
${{v}_{d}}$ is the drift velocity
$I$ is the current flowing through the conductor
$N$ is the charge density
$A$ is the area of cross section
$Q$ is the magnitude of charge

From the above equation we can see that,
${{v}_{d}}\propto \dfrac{1}{A}$

Drift velocity is inversely proportional to the area. Thus, the drift velocity will be minimum where the area is maximum. Therefore, the drift velocity is minimum at $z=0.5$
Therefore, the drift velocity is minimum in the middle of the conductor.

Hence, the correct option is (D).

Note:
The average velocity of all charges comes out to be zero. Charge flows from a region of high potential to a region of low potential. The drift velocity also depends on the electron mobility; it is the measure of how quickly an electron moves in a conductor or semiconductor. Electron mobility depends on temperature so drift velocity also depends on temperature.