Question

A conductor AB lies along the axis of a circular conducting loop C of radius r. If the current in the conductor AB varies at the rate of $x\,A/s$, then what is the induced emf in the coil?

A. $\dfrac{{{\mu }_{0}}rx}{2}$
B. $\dfrac{1}{4}\pi xr$
C. $\dfrac{{{\mu }_{0}}\pi xr}{2}$
D. zero

Answer 1

The magnitude of induced emf in a circuit is equivalent to rate of change in magnetic flux through the circuit. So, we will find the rate of change of the magnetic flux through the coil. The same value will be the induced emf in the coil.
Formula used:
Magnetic flux of a circuit, $\phi =\mathbf{B}.\mathbf{A}=BA\,\cos \theta$ ; Induced emf, $\epsilon =-\dfrac{d{{\phi }_{B}}}{dt}$

Complete answer:
Magnetic flux $\phi$ is the measurement of magnetic field passing normally through an area. Magnetic flux through an area is given by dot product of magnetic field and area vector.
$\phi =\mathbf{B}.\mathbf{A}$
$\phi =BA\,\cos \theta$
Where $\theta$ is the angle between magnetic field $\mathbf{B}$ and area vector $\mathbf{A}$.

Area vector is defined as the vector of a plane surface. Its magnitude is similar to that of the plane and direction is normal to that plane.

The magnitude of induced emf in a circuit is equivalent to rate of change in magnetic flux through the circuit. Therefore,
$\dfrac{d{{\phi }_{B}}}{dt}=\dfrac{dB}{dt}A\,\cos \theta$ (Since, area is not changing)
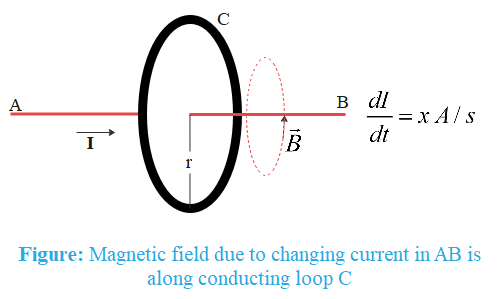
Direction of this magnetic field is given by the right hand thumb rule, which states that when we point the thumb of our right hand along the direction of current, the direction of curled fingers gives the direction of the magnetic field.
Applying this rule on straight wire AB, direction of magnetic field is as shown in figure.
The direction of magnetic field lines is always perpendicular to the area vector of the coil. Therefore, $\theta ={{90}^{{}^\circ }}$. This implies that
$\epsilon =-\dfrac{d\phi }{dt}=\dfrac{dB}{dt}A\,\cos {{90}^{{}^\circ }}=0$

So, the correct answer is “Option D”.

Note:
Moving charges can produce both electric and magnetic fields. Stationary charges do not produce magnetic fields.
Direction of the area vector is always normal to the plane of the surface. Sometimes students may assume the direction of the area vector along the diameter which will lead to the wrong result.