Question

A conducting wire of parabolic shape, $y={{x}^{2}}$, is moving with velocity $\overrightarrow{V}={{V}_{0}}\widehat{i}$ in a non-uniform magnetic field $\overrightarrow{B}={{B}_{0}}\left( 1+{{\left( \dfrac{y}{L} \right)}^{\beta }} \right)\widehat{k}$, as shown in the figure. If ${{V}_{0}},{{B}_{0}},L\text{ }$ and $\beta$ are positive constants and $\Delta \phi$ is the potential difference developed between the ends of the wire, then the correct statement(s) is/are?

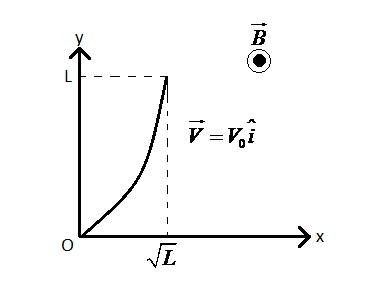
(This question has multiple correct options)
$A)\ \left| \Delta \phi \right|=\dfrac{4}{3}{{B}_{0}}{{V}_{0}}L\text{ for }\beta =2$
$B)\text{ }\left| \Delta \phi \right|$ remains the same if the parabolic wire is replaced by a straight wire, $y=x$, initially of length $\sqrt{2}L$
$C)\ \left| \Delta \phi \right|=\dfrac{1}{2}{{B}_{0}}{{V}_{0}}L\text{ for }\beta =0$
$D)\ \left| \Delta \phi \right|$ is proportional to the length of the wire projected on the y-axis.

Answer 1

The motional emf generated in the wire can be found out by integrating the infinitesimal emf developed in an infinitesimal part of the wire that is orthogonal to the velocity and the magnetic field, that is the infinitesimal length projected upon the y-axis and then integrating it for the whole wire.

Formula used:
$\left| \Delta \phi \right|=Bvl\sin \theta$

Complete step by step answer:
The motional emf $\left| \Delta \phi \right|$generated in a wire of length $l$ moving with a velocity $v$ in the presence of a magnetic field $B$ that is perpendicular to the plane of the wire and its velocity is given by
$\left| \Delta \phi \right|=Bvl\sin \theta$ --(1)
Where $\theta$ is the angle between the length of the wire and the direction of its velocity.
To find the motional emf generated in the wire, we have to consider the length of the wire that is perpendicular to the velocity and the magnetic field (that is component of the length along the y-axis). By doing this we will be essentially making $\theta ={{90}^{0}},\sin \theta =1$ in equation (1).
Hence, let us proceed to do that.
Let the infinitesimal emf generated in an infinitesimal vertical projection $dy$ of the length of the wire in the magnetic field $\overrightarrow{B}={{B}_{0}}\left( 1+{{\left( \dfrac{y}{L} \right)}^{\beta }} \right)\widehat{k}$ be $\left| d\varepsilon \right|$.
The velocity of the wire is $\overrightarrow{V}={{V}_{0}}\widehat{i}$.
Hence, using (1), we get
$\left| d\varepsilon \right|={{B}_{0}}{{\left( 1+\dfrac{y}{L} \right)}^{\beta }}{{V}_{0}}dy\sin {{90}^{0}}={{B}_{0}}\left( 1+{{\left( \dfrac{y}{L} \right)}^{\beta }} \right){{V}_{0}}dy\left( 1 \right)={{B}_{0}}\left( 1+{{\left( \dfrac{y}{L} \right)}^{\beta }} \right){{V}_{0}}dy$ $\left( \because \sin {{90}^{0}}=1 \right)$ --(2)
Now integrating (2), for the whole wire, we get
$\int\limits_{0}^{\left| \Delta \phi \right|}{\left| d\varepsilon \right|}=\int\limits_{0}^{L}{{{B}_{0}}\left( 1+{{\left( \dfrac{y}{L} \right)}^{\beta }} \right){{V}_{0}}dy}={{B}_{0}}{{V}_{0}}\int\limits_{0}^{L}{\left( 1+{{\left( \dfrac{y}{L} \right)}^{\beta }} \right)dy}$ --(3)
$\int\limits_{0}^{\left| \Delta \phi \right|}{\left| d\varepsilon \right|}={{B}_{0}}{{V}_{0}}\int\limits_{0}^{L}{\left( dy+{{\left( \dfrac{y}{L} \right)}^{\beta }}dy \right)}$

$\begin{aligned} & \int\limits_{0}^{\left| \Delta \phi \right|}{\left| d\varepsilon \right|}={{B}_{0}}{{V}_{0}}\left[ \left[ y \right]_{0}^{L}+\dfrac{1}{{{L}^{\beta }}}\left( \dfrac{{{y}^{\beta +1}}}{\beta +1} \right)_{0}^{L} \right]={{B}_{0}}{{V}_{0}}\left[ \left[ L-0 \right]+\dfrac{1}{{{L}^{\beta }}}\left( \dfrac{{{L}^{\beta +1}}-0}{\beta +1} \right)_{0}^{L} \right]={{B}_{0}}{{V}_{0}}\left[ L+\dfrac{1}{{{L}^{\beta }}}\left( \dfrac{{{L}^{\beta +1}}}{\beta +1} \right) \right] \\\ & ={{B}_{0}}{{V}_{0}}\left[ L+\left( \dfrac{L}{\beta +1} \right) \right]={{B}_{0}}{{V}_{0}}L\left( 1+\dfrac{1}{\beta +1} \right) \\\ \end{aligned}$
--- (4)
Now, let us analyze the options.
$A)\ \left| \Delta \phi \right|=\dfrac{4}{3}{{B}_{0}}{{V}_{0}}L\text{ for }\beta =2$. Let us check this.
Putting $\beta =2$ in (4), we get

$\left| \Delta \phi \right|=\dfrac{{{B}_{0}}{{V}_{0}}L}{{}}\left[ 1+\dfrac{1}{2+1} \right]={{B}_{0}}{{V}_{0}}L\left( 1+\dfrac{1}{3} \right)={{B}_{0}}{{V}_{0}}L\left( \dfrac{3+1}{3} \right)={{B}_{0}}{{V}_{0}}L\left( \dfrac{4}{3} \right)=\dfrac{4}{3}{{B}_{0}}{{V}_{0}}L$
Therefore, option (A) is correct.
$B)\text{ }\left| \Delta \phi \right|$ remains the same if the parabolic wire is replaced by a straight wire, $y=x$, initially of length $\sqrt{2}L$

If the wire is replaced by a straight wire length $\sqrt{2}L$, the vertical projection will be $\sqrt{2}L\sin {{45}^{0}}=\sqrt{2}L\times \dfrac{1}{\sqrt{2}}=L$ $\left( \because y=x,\text{ makes an angle of }{{45}^{0}}\text{ with the x-axis, }\sin {{45}^{0}}=\dfrac{1}{\sqrt{2}} \right)$
Hence, we can see that the vertical projection is still $L$ which is the same as that of the parabolic wire as can be seen from (4). Therefore, $\left| \Delta \phi \right|$ will remain the same.

$C)\ \left| \Delta \phi \right|=\dfrac{1}{2}{{B}_{0}}{{V}_{0}}L\text{ for }\beta =0$
Putting $\beta =0$ in (4), we get
$\left| \Delta \phi \right|=\dfrac{{{B}_{0}}{{V}_{0}}L}{{}}\left[ 1+\dfrac{1}{0+1} \right]={{B}_{0}}{{V}_{0}}L\left( 1+\dfrac{1}{1} \right)={{B}_{0}}{{V}_{0}}L\left( 2 \right)=2{{B}_{0}}{{V}_{0}}L$
Hence, option C) is wrong.
$D)\ \left| \Delta \phi \right|$ is proportional to the length of the wire projected on the y-axis.
From (4), we can see that $\left| \Delta \phi \right|$ is proportional to the length of the wire projected on the y-axis.
Therefore, option D) is correct.

Note:
Complex problems involving motional emf should be approached by finding out the length, velocity and magnetic fields and placing them such, by taking components or otherwise so that a mutually orthogonal system is obtained. Then we can find the motional emf by integration of an infinitesimal length of the wire. This will make the problem a lot easier and give a direction for the students to proceed when faced with such problems that seem overwhelming at the first glance.