Question

A conducting wire of length $l$ and mass $m$ can slide without friction on two parallel rails and is connected to capacitance $C$. Whole system lies in a magnetic field $B$ and a constant force $F$ is applied to the rod. Then

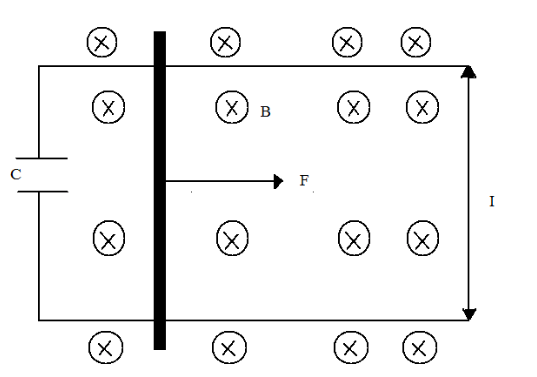
This question has multiple correct options
A) The rod moves with constant velocity
B) The rod moves with an acceleration of $\dfrac{F}{{m + {B^2}{l^2}c}}$
C) There is constant charge on the capacitor
D) Charge on the capacitor increases with time
E) Answer required

Answer 1

In order to solve this question, one should be aware of the concept of emotional EMF and here, there are two forces acting on the moving wire and both the forces would be opposite of each other. One force is given in the question and the second one would be due the magnetic field and the current.

Complete Step by Step Answer:
Here, the concept of emotional EMF would be there.
Let at any instant, the rod is moving with velocity $v$ towards right due to force $F$ and acceleration of the wire be $a$ at that instant $a = \dfrac{{dv}}{{dt}}$​

Thus the EMF induced $E = Bvl$
Therefore, Charge flows across the loop
$q = C \times E$
$q = CBvl$ (Equation 1)
The current flows in the loop in anti-clockwise direction
As we know that, $i = \dfrac{{dq}}{{dt}}$
The direction in which this current will flow would be anti-clockwise.
Putting the expression for $q$ we have,
$i = BlC\dfrac{{dv}}{{dt}}$
As we know that $a = \dfrac{{dv}}{{dt}}$ Therefore, we have
$i = BlCa$

As the net force acting on a closed loop is the difference of the force applied on the loop through which it is getting its velocity and the force acting on it due to the magnetic field. As the direction of both the forces is opposite.
Hence we have, the force ${F'} = Bil$ acts towards the left.
So, the net force would be
$ma = F - Bil$
Putting the expression for $i$ in the above equation we have,
$ma = F - B(BiCa)l$
Putting $a$ on one side and other expression on the other side we have,
$a = \dfrac{F}{{m + {B^2}{l^2}C}}$

As acceleration is constant, hence $v$ increases with time.
In option A we are given that the rod moves with constant velocity so it is wrong as we just deduced that velocity would increase with time. So, option B is correct.
From equation 1, which says
$q = CBvl$
So, the charge on the capacitor will increase with time. So, option C is wrong and option D is right.

Hence, options B and D are correct.

Note: As the wire moves in the magnetic field there would be a change in the magnetic flux and this change in the magnetic flux will induce an EMF that will be opposing that change and this whole process is known as induction.