Question

A conducting square loop of side L and resistance R moves in its plane with a uniform velocity v perpendicular to its side. A magnetic induction B, constant in time and space, pointing perpendicular and into the plane exists everywhere. The current induced in the loop is

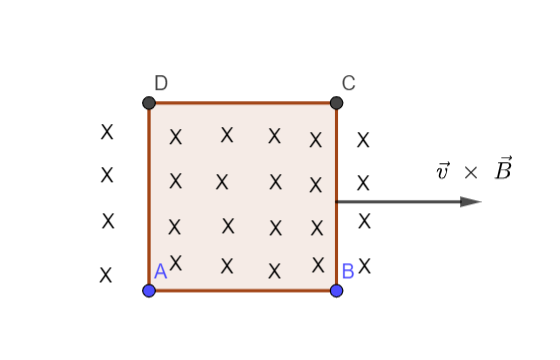
A. $\dfrac{{Blv}}{R}$ clockwise
B. $\dfrac{{Blv}}{R}$ anti-clockwise
C. $\dfrac{{2Blv}}{R}$ anti-clockwise
D. zero

Answer 1

Here we shall apply the concept of electromagnetic induction. Faraday's laws explain the behavior of a conductor when placed in a varying magnetic field. We will first calculate the change in flux linked to the conductor when it is placed in the magnetic induction. Using appropriate formulas as derived from Faraday's laws, we will get the value of induced emf. Hence, we will then calculate the value of the induced current.

Complete step by step solution:
Faraday’s laws predict how a magnetic induction would interact with current to produce an electromotive force abbreviated as emf. The Faraday’s laws state that
(1) The induced emf and hence the induced current is set up in a conductor if it is placed in a varying magnetic field.
(2) The magnitude of this induced emf is given by the rate of change of flux experienced by the conductor.
Accordingly, if we analyze the given situation, we will see that the flux linked to the conducting square loop of side L and resistance R is zero since the conductor is wholly placed in the region where magnetic induction is present. The number of magnetic field lines associated with the loop do not change because the loop is completely resting in a region of magnetic induction. So, the magnetic flux associated with the loop does not change as long as the loop is completely within the region.
So, we can say that $d\phi = 0$ where $\phi$ denotes the flux linked to the loop at a given time t.
The emf is given by $e = - \dfrac{{d\phi }}{{dt}}$ .
Substituting the value of flux change, we get,
$e = 0$
Since the induced emf is zero, the induced current will also be zero as there is no potential gradient along which the current would flow.
Hence, option D is the correct answer.

Note:
In this question, we only focused on the magnitude of the induced emf. The direction of the induced emf is given by Lenz’s law which states that the direction of the emf is such that it always opposes the cause of the change. It follows the principle of conservation of energy and is applicable universally without any limitations.