Question

A conducting sphere of radius r has a charge. Then:
A. The charge is uniformly distributed over its surface, if there is an external field.
B. Distribution of charge over its surface will be non uniform if no external electric field exists in space.
C. Electric field strength inside the sphere will be equal to zero only when no external electric field exists.
D. Potential at every point on the sphere must be the same.

Answer 1

We know when a conductor is kept in an electric field, it experiences an electric force. Different situations of a conducting sphere are given in the question. We discuss each case to find the correct one.

Complete answer:
We have a conducting sphere, and the radius of the sphere is given as ‘r’.
We are given four cases in the question.
Let us consider the 1st case.
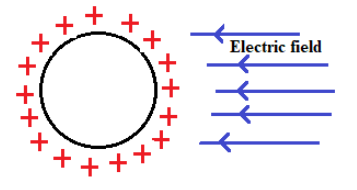
In this case, it is said that when we have an external electric field the charge in the conducting sphere will get uniformly distributed over the surface.

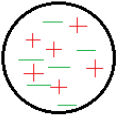
Consider a conducting sphere as shown in the above sphere.
When we move this sphere to a place with an external electric field,

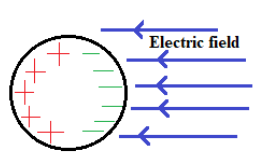
The charge in the sphere gets rearranged at the surface of the sphere as shown in the figure.
Therefore the first case is wrong.
Now, let us look into the 2nd case.
In this case, it is said when there is no external electric field; the charge on a conductor will be distributed non-uniformly over its surface.
Now let us consider a conducting sphere, not in an electric field

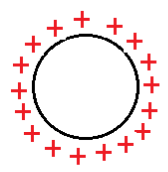
When the sphere is not in an electric field, charge is distributed uniformly over the surface.
Therefore case two is also wrong.
Now consider the 3rd case.
It is said that electric field strength inside the will be zero only if there is no electric field.
When a sphere is not in an electric field,

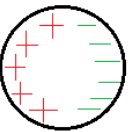
The two equal and opposite charges get cancelled and total strength becomes zero.
When it is in an electric field,

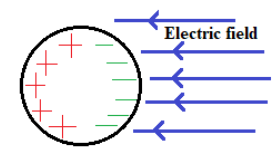
In this situation also, the charges get cancelled and total strength becomes zero.
Therefore, even if the conductor is in an electric field or not, the electric field strength inside the conductor will be zero.
Therefore it proves the 3rd case is also wrong.
Now let us consider the 4th case.
In this case it said that the potential at every point on the surface will be equal.
Let us consider a conducting sphere.
We know that if the sphere is not in an electric field, the charge is uniformly distributed over the surface; hence the potential at every point on the surface will be the same.
If the sphere is in an electric field,

The electric field will be perpendicular to the charge at the surface; hence the potential the surface will be zero.
As we know, the surface of the conductor will be equipotential.
Therefore this case is correct.

Hence the correct answer is option D.

Note:
The electric field is the region the force is felt. The amount of work required to move a unit charge from a reference point to a specific point against the electric field.
We might think that if there is no electric field, the charge will be non-uniformly distributed over the surface of the sphere. This assumption is wrong.
When there is no electric field the charge will be distributed uniformly over the surface of the conductor. Don’t be confused.