Question

: A conducting sphere of radius R and a concentric thick spherical shell of inner radius 2R and outer radius 3R is shown in figure. A charge +10Q is given to the shell and the inner sphere is earthed. The charge on inner sphere is

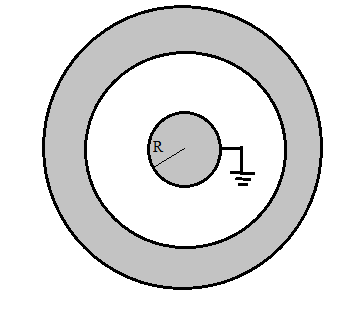
A. -4Q
B. -10Q
C. zero
D. none

Answer 1

The arrangement of the conductors is such that they form a spherical capacitor. Since we earthed the inner sphere, the potential difference between this sphere and the ground becomes zero i.e, the inner sphere is at a potential of V = 0.

Complete answer:
We are given that the inner sphere of radius R is earthed and surrounding it there is a spherical shell with inner radius 2R and Outer radius 3R. When a charge of +10Q is imparted to spherical shell (outer), this gets divided into two parts:
1. A charge $q_i$ gets distributed on the inner surface of the shell of radius 2R.
2. A charge of $q_o$ gets distributed on the outer surface of the shell with radius 3R.

Due to a charge $q_i$ on the inner surface of the shell, a charge $- q_i$ gets induced on the inner sphere of radius R.
The potential $V_B$ on the outer surface of the shell due to the outward electric field intensity is:
$V_B = \dfrac{q_o + q_i - q_i }{4 \pi \epsilon_0 3R}$
We keep $q_o - q_i = 10Q$, we get the potential difference as:
$V_B - V_A = \dfrac{+10Q + q_i }{4 \pi \epsilon_0 3R}$ .
Where $V_A$ is zero (inner shell).

The inner surface of the shell should contribute some potential difference given by:
$V_B - V_A = \dfrac{q_i }{4 \pi \epsilon_0} \left( \dfrac{1}{R} - \dfrac{1}{2R} \right)$

Equating the two potential differences, we get:
$\dfrac{+10Q + q_i }{4 \pi \epsilon_0 3R} = \dfrac{q_i }{4 \pi \epsilon_0} \left( \dfrac{1}{R} - \dfrac{1}{2R} \right)$
Or, we can simplify this as:
$\dfrac{+10Q + q_i }{q_i} = \dfrac{3R(2R-R)}{2R^2}$
Which gives us:
$q_i = 4Q$
Since in the beginning of the discussion, we saw that $- q_i$ gets distributed on the inner shell.
So, the correct answer is “Option A”.

Note:
One potential difference is derived by integrating net Electric field outward and another is derived from net electric field inwards (between the inner sphere and outer shell). We equated the two potential differences i.e., one at a point outside the arrangement and one in between the two spheres.