Question

A conducting sphere of radius $a$ has a charge $Q$ on it. It is enclosed by a neutral concentric spherical shell having an inner radius $2a$ and outer radius $3a$ . Find the electrostatic energy of the system.
A) $\dfrac{5}{{12}}\dfrac{{{Q^2}}}{{4\pi {\varepsilon _0}a}}$
B) $\dfrac{{11}}{{12}}\dfrac{{{Q^2}}}{{4\pi {\varepsilon _0}a}}$
C) $\dfrac{1}{2}\dfrac{{{Q^2}}}{{4\pi {\varepsilon _0}a}}$
D) $\dfrac{1}{{12}}\dfrac{{{Q^2}}}{{4\pi {\varepsilon _0}a}}$

Answer 1

The given system can be considered to be three concentric spherical shells of radii $a$, $2a$ and $3a$. The charge $Q$ on the conducting sphere will induce a charge $- Q$ on the second spherical shell which then induces a charge $Q$ on the third spherical shell. Then the total electrostatic energy of the system will be the sum of the self-potential energy of each sphere and the energy of interaction between the spheres.

Formulas used:
The electrostatic potential energy of a sphere of charge $q$ is given by, $U = \dfrac{{{q^2}}}{{4\pi {\varepsilon _0}\left( {2r} \right)}}$ where $r$ is the radius of the sphere.
The electrostatic potential energy of a charge $q$ in an external potential $V$ is given by, $U = Vq$ .
The potential at a point due to a charge $q$ is given by, $V = \dfrac{q}{{4\pi {\varepsilon _0}r}}$ where $r$ is the distance between the point and the charge.

Complete step by step answer:
Step 1: Sketch a figure describing the system under consideration.
It is given that a conducting sphere with some charge is enclosed within a concentric spherical shell which is neutral. This system is considered as three concentric spherical shells. This is shown in the figure below.

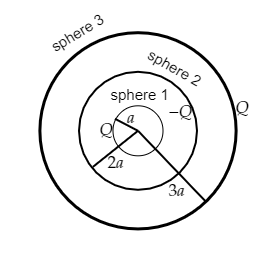
As seen in the above figure, the sphere 1 has a radius ${r_1} = a$ and charge $Q$ on it, the sphere 2 has a radius ${r_2} = 2a$ and charge $- Q$ on it and the sphere 3 has a radius ${r_3} = 3a$ and charge $Q$ on it.
The electrostatic potential energy of a sphere of charge $q$ is given by, $U = \dfrac{{{q^2}}}{{4\pi {\varepsilon _0}\left( {2r} \right)}}$ where $r$ is the radius of the sphere.
Then the electrostatic potential energies of sphere 1 will be ${U_1} = \dfrac{{{Q^2}}}{{4\pi {\varepsilon _0}\left( {2a} \right)}}$ , that of sphere 2 will be ${U_2} = \dfrac{{{Q^2}}}{{4\pi {\varepsilon _0}\left( {2 \times 2a} \right)}}$ and that of sphere 3 is ${U_3} = \dfrac{{{Q^2}}}{{4\pi {\varepsilon _0}\left( {2 \times 3a} \right)}}$ .
Now the electrostatic energy of the system will be the sum of the potential energy of each sphere and the interaction energy between the spheres.
Step 2: Express the potential energy of the system due to interaction between the spheres.
The potential at a distance $r$ due to a charge $q$ is given by, $V = \dfrac{q}{{4\pi {\varepsilon _0}r}}$ where $r$ is the distance between the point and the charge.
The potential of charge $Q$ at distance $r = 2a$ can be expressed as
${V_1} = \dfrac{Q}{{4\pi {\varepsilon _0}2a}}$ ------- (1)
The potential of charge $Q$ at a distance $r = 3a$ can be expressed as
${V_3} = \dfrac{Q}{{4\pi {\varepsilon _0}\left( {3a} \right)}}$ ------- (2)
So the interacting potential energy between spheres 1 and 2 can be expressed as
${U_{12}} = {V_1}\left( { - Q} \right)$ ------- (3)
Substituting equation (1) in (3) we get, ${U_{12}} = \dfrac{{ - {Q^2}}}{{4\pi {\varepsilon _0}\left( {2a} \right)}}$
So the interacting potential energy between spheres 1 and 2 is ${U_{12}} = \dfrac{{ - {Q^2}}}{{4\pi {\varepsilon _0}\left( {2a} \right)}}$ ------- (4)
Similarly, the interaction potential energy between spheres 1 and 3 can be expressed as ${U_{31}} = {V_3}Q = \dfrac{{{Q^2}}}{{4\pi {\varepsilon _0}\left( {3a} \right)}}$ --------- (5)
And the interaction potential energy between sphere 2 and 3 will be
${U_{23}} = {V_3}\left( { - Q} \right) = \dfrac{{ - {Q^2}}}{{4\pi {\varepsilon _0}\left( {3a} \right)}}$ --------- (6)
Then the potential energy due to interaction will be ${U_{\operatorname{int} eraction}} = {U_{12}} + {U_{31}} + {U_{23}}$
Substituting equations (4), (5) and (6) in the above expression we get, ${U_{\operatorname{int} eraction}} = \dfrac{{ - {Q^2}}}{{4\pi {\varepsilon _0}\left( {2a} \right)}} + \dfrac{{{Q^2}}}{{4\pi {\varepsilon _0}\left( {3a} \right)}} + \dfrac{{ - {Q^2}}}{{4\pi {\varepsilon _0}\left( {3a} \right)}}$
$\Rightarrow {U_{\operatorname{int} eraction}} = \dfrac{{ - {Q^2}}}{{4\pi {\varepsilon _0}a}}\left( {\dfrac{1}{2}} \right)$
Thus the interaction energy is ${U_{\operatorname{int} eraction}} = \dfrac{{ - {Q^2}}}{{4\pi {\varepsilon _0}a}}$ --------- (A) .
Step 3: Express the potential energy of the system.
The electrostatic energy of the system will be ${U_T} = {U_{self}} + {U_{\operatorname{int} eraction}}$ ------- (7)
Here the self-energy of the system will be the sum of the potential energies of the spheres themselves.
i.e., ${U_{self}} = {U_1} + {U_2} + {U_3}$
Substituting for ${U_1} = \dfrac{{{Q^2}}}{{4\pi {\varepsilon _0}\left( {2a} \right)}}$ , ${U_2} = \dfrac{{{Q^2}}}{{4\pi {\varepsilon _0}\left( {2 \times 2a} \right)}}$ and ${U_3} = \dfrac{{{Q^2}}}{{4\pi {\varepsilon _0}\left( {2 \times 3a} \right)}}$ in the above relation we get, ${U_{self}} = \dfrac{{{Q^2}}}{{4\pi {\varepsilon _0}\left( {2a} \right)}} + \dfrac{{{Q^2}}}{{4\pi {\varepsilon _0}\left( {2 \times 2a} \right)}} + \dfrac{{{Q^2}}}{{4\pi {\varepsilon _0}\left( {2 \times 3a} \right)}}$
$\Rightarrow {U_{self}} = \dfrac{{{Q^2}}}{{4\pi {\varepsilon _0}a}}\left[ {\dfrac{1}{2} + \dfrac{1}{4} + \dfrac{1}{6}} \right]$ --------- (B)
Now, substituting equations (A) and (B) in equation (7) we get, ${U_T} = \dfrac{{{Q^2}}}{{4\pi {\varepsilon _0}a}}\left[ {\dfrac{1}{2} + \dfrac{1}{4} + \dfrac{1}{6}} \right] + \dfrac{{ - {Q^2}}}{{4\pi {\varepsilon _0}a}}\left[ {\dfrac{1}{2}} \right]$
$\Rightarrow {U_T} = \dfrac{{{Q^2}}}{{4\pi {\varepsilon _0}}}\left[ {\dfrac{1}{2} + \dfrac{1}{4} + \dfrac{1}{6} - \dfrac{1}{2}} \right] = \dfrac{5}{{12}}\dfrac{{{Q^2}}}{{4\pi {\varepsilon _0}}}$
Thus the total electrostatic energy of the system is
$\Rightarrow {U_T} = \dfrac{5}{{12}}\dfrac{{{Q^2}}}{{4\pi {\varepsilon _0}}}$

Hence the correct option is A.

Note:
For a conducting sphere, charge resides only on the surface of the sphere. Here it is mentioned that the concentric shell which encloses the conducting sphere is neutral. Then the charges induced at each surface of the shell will have the same magnitude but opposite signs so that the shell as a whole remains to be neutral.