Question

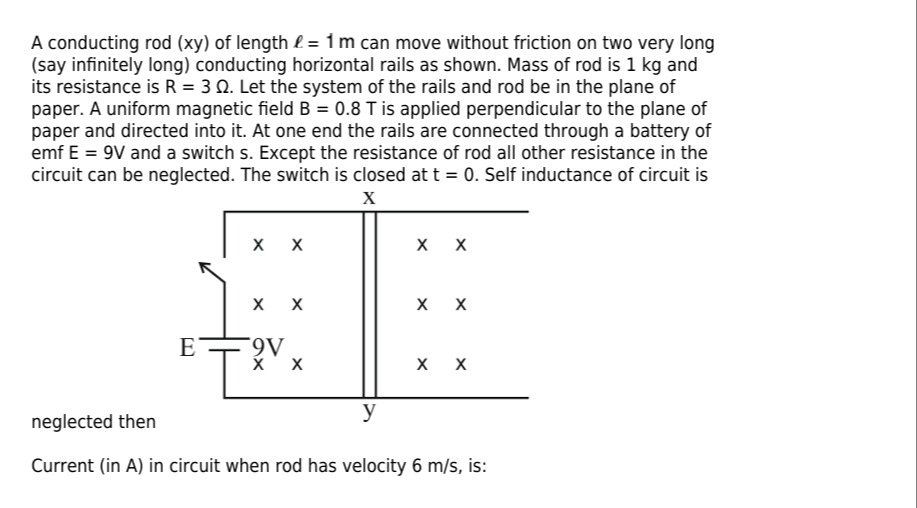
A conducting rod (xy) of length $\ell$ = 1 m can move without friction on two very long (say infinitely long) conducting horizontal rails as shown. Mass of rod is 1 kg and its resistance is R = 3 $\Omega$. Let the system of the rails and rod be in the plane of paper. A uniform magnetic field B = 0.8 T is applied perpendicular to the plane of paper and directed into it. At one end the rails are connected through a battery of emf E = 9V and a switch s. Except the resistance of rod all other resistance in the circuit can be neglected. The switch is closed at t = 0. Self inductance of circuit is

neglected then

Current (in A) in circuit when rod has velocity 6 m/s, is:

Answer 1

1.4

Answer 2

The circuit contains a battery and a moving rod in a magnetic field. The moving rod induces a motional emf $\mathcal{E}_{ind} = B\ell v$. This induced emf opposes the battery emf E. The net emf in the circuit is $E - \mathcal{E}_{ind}$. The current in the circuit is given by Ohm's law: $I = \frac{\text{Net emf}}{\text{Total resistance}} = \frac{E - B\ell v}{R}$. Substitute the given values $E=9\text{V}$, $B=0.8\text{T}$, $\ell=1\text{m}$, $v=6\text{m/s}$, and $R=3\Omega$ to find the current.

$\mathcal{E}_{ind} = (0.8)(1)(6) = 4.8\text{V}$.

$I = \frac{9 - 4.8}{3} = \frac{4.2}{3} = 1.4\text{A}$.