Question
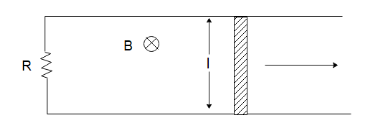
Question: A conducting rod moves towards the right with constant velocity \(v\) in a uniform transverse magnet...
A conducting rod moves towards the right with constant velocity v in a uniform transverse magnetic field. The graph between the force applied by the external agent v/s velocity and power supplied by the external agent v/s velocity is:
A) Straight line, parabola
B) Parabola, straight line
C) Straight line, straight line
D) Parabola, Parabola
Solution
In this solution, we will understand the concepts of Lenz law and electromagnetic induction. When the rod moves towards the right, the flux enclosed by the rod increases which will be opposed due to Lenz law, and we will have to apply external force.
Formula used: In this solution, we will use the following formula:
-Flux passing through the region enclosed by the rod: ϕ=Blx where B is the external magnetic field, l is the length of the rod, and x is the displacement of the rod.
- Induced EMF V=dtdϕ
- Current in the circuit I=RV where R is the resistance in the circuit.
- Force on a current-carrying object in a magnetic field F=BIl
Complete step by step answer:
When the conducting rod moves to the right the flux enclosed by the surface increases. This change in flux will be opposed due to Lenz law. To keep the rod moving to the right, we will have to apply an external force that can overcome the force exerted by Lenz law. Let us start by calculating the flux enclosed by the surface.
We know that the flux enclosed by the surface will be
ϕ=Blx
The EMF that will be induced in the system will be the rate of change of flux with respect to time. So,
V=dtdϕ
Since the only changing expression in the flux is the displacement of the rod with respect to time, we can differentiate the flux and write
V=dtd(Blx)
⇒V=BLv where v is the velocity of the rod.
Then if the resistance of the entire system is R, the current in the circuit can be determined through ohm’s law as
I=RV
⇒I=RBlv
Then the force that has to be acted on the rod will be equal to
F=BIl
⇒F=RB2l2v
Thus F∝v. This is the relation that corresponds to a straight line.
Now, the power in the circuit (P) will be a product of the external force that is applied and the velocity of the rod i.e.
P=Fv
Which gives us
P=RB2l2v2
So, P∝v2 . This is the relation that corresponds to a parabola.
Hence option (A) is the correct choice.
Note: In such questions, we must be familiar with the laws of electromagnetic induction, basic circuit theory, and Lorentz forces. The formulae we have used here are only applicable if the entire circuit is perpendicular to the direction of the magnetic field since otherwise, we would have to take the component of the area enclosed that is perpendicular to the magnetic field.
