Question

A conducting ring of mass $2\,kg$ and radius $0.5\,m$ is placed on a smooth horizontal plane. The ring carries current $i = 4\,A$ . A horizontal magnetic field $B = 10\,T$ is switched on at $t = 0$ as shown in the figure. The initial acceleration is:
A.$40\pi \,rad\,{s^{ - 2}}$
B.$20\pi \,rad\,{s^{ - 2}}$
C.$5\pi \,rad\,{s^{ - 2}}$
D.$15\pi \,rad\,{s^{ - 2}}$

Answer 1

Here, we will use the formula of torque to calculate the initial acceleration of the ring. Torque is defined as a measure of force that is required to rotate an object about its axis. Also, torque can be defined as the product of moment of inertia and acceleration produced in the ring.

FORMULA USED: The formula of torque is given by
$\tau = \vec M \times \vec B$
Here, $\tau$ is the torque, $M$ is the magnetic moment and $B$ is the magnetic field.
Also, the formula of torque used to calculate the acceleration is given by
$\tau = I\alpha$
Here, $I$ is the moment of inertia and $\alpha$ is the acceleration.

COMPLETE STEP BY STEP ANSWER:
Consider a conducting ring of radius $0.5\,m$ and having mass $2\,kg$ . let this ring be placed on a smooth horizontal plane. As shown below

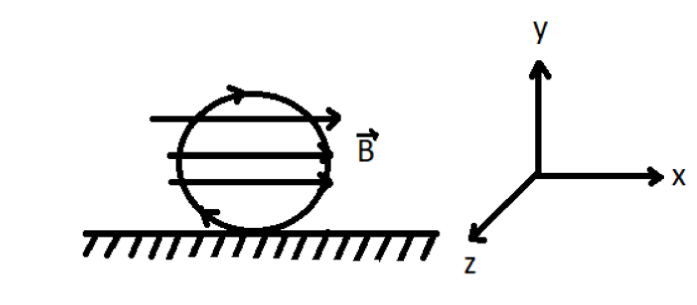
(Self-made diagram)

Now, to calculate the initial acceleration of the conducting ring, we will first calculate the torque in the ring.
Torque is defined as a measure of force that is required to rotate an object about its axis. The formula of the torque is given below

$\tau = \vec M \times \vec B$
$\Rightarrow \,\tau = MB\sin \theta$
Now, magnetic moment $M$ is defined as the product of current flowing through a conductor and the area of the conductor, which is shown below
$M = iA$

Now, area of the conductor is $A = \pi {r^2}$
Therefore, magnetic moment will become
$M = i\pi {r^2}$
Putting this value in the equation of torque, we get
$\tau = \left( {i\pi {r^2}} \right)B\sin \theta$
$\Rightarrow \,\tau = \left( {i\pi {r^2}} \right)B\sin 90^\circ$
$\Rightarrow \,\tau = 4 \times \pi \times {\left( {0.5} \right)^2} \times 10 \times 1$
$\Rightarrow \,\tau = 4 \times \pi \times 0.25 \times 10 \times 1$
$\Rightarrow \,\tau = 10\pi \,Nm$

Now, to calculate the initial acceleration of the ring, we will use the torque formula that is the product of moment of inertia and acceleration produced.
$\tau = I\alpha$
Now, moment of inertia, $I = m{r^2}$

Therefore, torque in the ring will become
$\tau = \left( {m{r^2}} \right)\alpha$
$\Rightarrow \,10\pi = 2 \times 0.25 \times \alpha$
$\Rightarrow \,\alpha = \dfrac{{10\pi }}{{2 \times 0.25}}$
$\Rightarrow \,\alpha = \dfrac{{10\pi }}{{0.5}}$
$\Rightarrow \,\alpha = 20\pi$
Therefore, the initial acceleration produced in the ring is $20\pi \,rad\,{s^{ - 2}}$ .

Hence. Option (B) is the correct option.

NOTE: Here, in the above question we can also take $\mu$ as the magnetic momentum instead of $M$ .

Hence, the formula of torque will become $\tau = \vec \mu \times \vec B$ .
Here, the ring is moving on the smooth surface that is why we have used the formula of torque to calculate acceleration.