Question

A conducting circular loop of radius $r$ carries a constant current $i$. It is placed in a uniform magnetic field $\overrightarrow {{B_o}}$ perpendicular to the plane of the loop. The magnetic force acting on the loop is
A. $ir{B_o}$
E. $2\pi ir{B_o}$
F. Zero
G. $\pi ir{B_o}$

Answer 1

Firstly Find the force acting on each small element on the circular loop due to the magnetic force and check for the direction of force using right hand rule. Consider the net force on each element of the loop.

Complete Step by step answer: Given, radius of the loop is $r$
Current through the loop is $i$
Magnetic field vector is $\overrightarrow {{B_o}}$

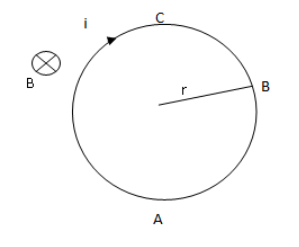
Let us consider a small arc ABC
The force on a current carrying conductor due to a magnetic field is given as,
$\overrightarrow F = I\left( {\overrightarrow {dl} \times \overrightarrow B } \right)$
Therefore force on arc ABC due to the magnetic field will be,
$\overrightarrow F = i\left( {\overrightarrow {dl} \times \overrightarrow {{B_o}} } \right)$
Using the right hand rule, we observe that the force is acting towards the centre.
Similarly, for every element of the circular loop the force will act towards the centre and each force on an element of the loop will get cancelled by the force acting on the opposite side of the loop. Thus, the net force will be zero.

Hence, the correct answer is option (C) zero.

Note: Force acting on a conductor with closed loop due to a uniform magnetic field acting perpendicular to the loop is always zero. However if the magnetic field is changing with time or it is not a closed loop, then there will be some net force acting on the conductor.