Question
Question: A condenser of \(2\mu F\) capacitor is charged at uniform rate from zero to \(5\mu C\). Which of the...
A condenser of 2μF capacitor is charged at uniform rate from zero to 5μC. Which of the following curves correctly represent the variation of potential difference across the plates with respect to the charge on the condenser?
(A)
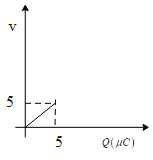
(B)
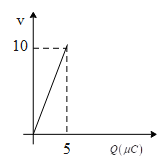
(C )
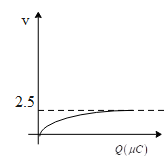
(D)
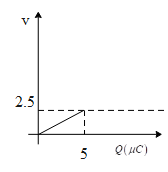
Solution
The charge and voltage is directly proportional. That is, the charge is the product of capacitance and the potential difference. So the curve should always be a straight line. Hence, calculate the voltage when the capacitor is fully charged. Thus potential can be calculated by taking the ratio of Q to C. Thus substituting the values we will get the final potential and from this we can analyse the shape of the graph.
Formula used:
Q=CV
where, Q is the charge
C is the capacitance
V is the potential difference
Complete step by step solution:
Q=CV…………….(1)
where, Q is the charge
C is the capacitance
V is the potential difference
By rearranging equation (1) we get,
V=CQ
Hence the voltage when the capacitor is fully charged is given by,
Vf=CQ
Substituting the values we get,
Vf=25∴Vf=2.5V
Thus, the potential difference or voltage across the capacitor should remain constant.
Therefore option (D) is correct.
Additional information:
The charge and voltage is directly proportional. That is, the charge is the product of capacitance and the potential difference. So the curve should always be a straight line.
Note:
The capacitance of the capacitor is affected by two factors. That is, the area of the plate, the distance between the two plates. In the case of larger plates the capacitance will store greater electric charge. As the area of the plate increases the capacitance also increases. Hence, the capacitance can also be described as the capacity to store energy as electrical charge. The value of capacitance is always positive. It never has a negative value.
