Question

A concave mirror produces a real image twice the size of the object when placed at a distance of 22.5 cm from it. Where should the object be placed so that the size of the image becomes three times that of the object?
A. 20 cm
B. 22.5 cm
C. 30.4 cm
D. 24 cm

Answer 1

In case of mirrors usually there are three types used. Plain mirror, concave mirror and convex mirror. All will serve different purposes. Properties of different mirrors are different. In case of convex mirrors they always form virtual images. While concave mirrors form both virtual and real images and plain mirrors form virtual images. Inverted image in the sense it is real. Whatever may be the orientation we have a magnification formula to determine the size of the image.

Formula used:
$m = \dfrac{{ - v}}{u} = \dfrac{f}{{f - u}}$

Complete step by step answer:
Various positions of placing an object in front of a concave mirror gives us various positions of images.
If an object is placed between the pole and focus of the concave mirror then image will be formed on the other side of the mirror. That image formed can be enlarged or diminished and virtual.
Now if we place an object between focus and center then the image is formed away from the center and the image will be real and inverted. The size of the image will be bigger than an object as shown in the diagram.

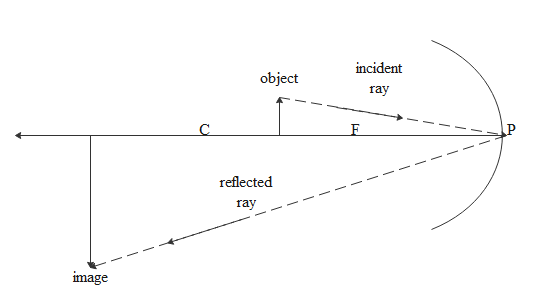
If the object is placed exactly at center the image also will be formed exactly at the center just as shown in the diagram below.

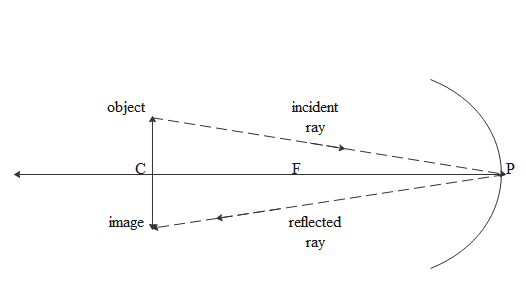
P denotes the pole and F denotes the focus and C denotes the center.
The magnification produced due to the concave mirror is given as 2. Since it is real image and magnified, it will fall under the first case we discussed with the diagram. So the image will be inverted and magnified. So magnification with proper sign will be -2. Object distance with sign is -22.5 cm.
Formula for the magnification is
$m = \dfrac{{ - v}}{u} = \dfrac{f}{{f - u}}$
Where ‘u’ is the object distance and ‘v’ is the image distance and ‘f’ is the focal length and ‘m’ is the magnification. Since image distance is not given we will continue with the formula
\eqalign{ & m = \dfrac{f}{{f - u}} \cr & \Rightarrow - 2 = \dfrac{f}{{f - ( - 22.5)}} \cr & \Rightarrow - 2f - 45 = f \cr & \Rightarrow 3f = - 45 \cr & \therefore f = - 15 \cr}
Now the required magnification is -3
\eqalign{ & m = \dfrac{f}{{f - u}} \cr & \Rightarrow - 3 = \dfrac{{ - 15}}{{ - 15 - (u)}} \cr & \Rightarrow 5 = - 15 - u \cr & \therefore u = - 20cm \cr}
Negative sign indicates the object is in front of the mirror.
Hence objects must be placed 20cm in front of the mirror to get the magnification 3.
Hence option A will be the answer.

Note:
The image which we get in the final process is the inverted real enlarged image. If we need to get the virtual enlarged image of the same magnification then we should put the object between the pole and the focus of the mirror. If we put an object between the center and focus of the mirror we get an inverted magnified image.