Question

A concave mirror of focal length $'{f_1}'$ is placed at a distance of $'d'$ from a convex lens of focal length $'{f_2}'$. A beam of light coming from infinity and falling on this convex lens concave mirror combination returns to infinity. The distance $'d'$ must equal to:
(A) $2{f_1} + {f_2}$
(B) $- 2{f_1} + {f_2}$
(C) ${f_1} + {f_2}$
(D) $- {f_1} + {f_2}$

Answer 1

Consider a combination of convex lens and concave mirror with convex lens placed to the left.

The light coming from infinity goes back to infinity. So, you are supposed to find a way or a point such that the light is reflected back and goes to infinity. In order to do this, trace the path of the light as it passes through the combination and make it go back to infinity and then accordingly, find the distance $'d'$.

Complete step by step solution:
Consider a ray of light coming from infinity, it will first hit the convex lens, get refracted and finally an image will be formed at the focus of the convex lens. The focus of the convex will be to the right of the pole of the lens and at a distance of$'{f_2}'$.

Now, whenever an object is placed at the centre of curvature of a concave mirror, the image formed will be real, inverted, of same size and at the centre of curvature.

If the first image formed by the convex lens acts as object for the concave mirror, then due to
reflection at the concave mirror, the image of this object (which is the image due to convex lens) will form at the same position which is the centre of curvature of the concave mirror.

Now the second image formed by the concave mirror (which is at the centre of curvature of the concave mirror) will act as an object for the convex lens and whenever an object is placed at the focus of the convex lens, the image will form at infinity. Therefore, the final image of the object which is placed at infinity will form at infinity and also at the same side. Schematic diagram is shown for the purpose of understanding.

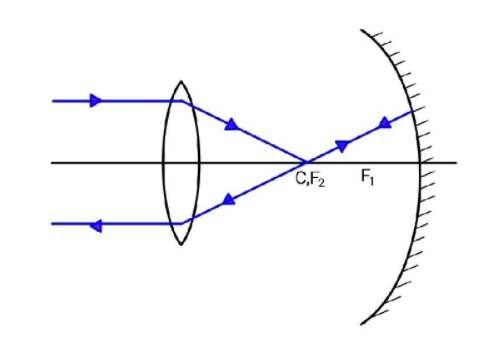
So, the first image will form at $'{f_2}'$, then the concave mirror is to be placed such that the centre of curvature of the mirror coincides with the focus of the lens, then second image will be formed at the centre of curvature and then finally the third image will form at infinity, meaning that the light will go back to infinity.

The centre of curvature of a concave mirror is located at a distance of $R = 2{f_1}$, where $R$ is the radius of curvature. As from the figure you can see, the distance $d$ has to be the sum of the radius of curvature and the focus of the convex lens which is ${f_2}$. Therefore $d = 2{f_1} + {f_2}$.

Hence, the distance $'d'$ must equal $2{f_1} + {f_2}$.

Hence ,Option (A) is correct.

Note: There are two focuses of a convex lens. These are located on both sides of the lens. Here we only considered the focus on the right side. Considering the left focus will lead to wrong answers.

Remember that, whenever a ray of light is coming from infinity, then due to a convex lens, the light will be focused at the focus. Whenever a ray of light passes through the centre of curvature of a concave mirror, the light will reflect and will again pass through the centre of curvature.