Question

A concave mirror of focal length $20cm$ is placed $50cm$ from a wall. How far from the wall where the object should be placed to form its real image on the wall?

Answer 1

The distance of the object from the mirror is to be calculated here first. According to the mirror equation,

$\dfrac{1}{f}=\dfrac{1}{v}+\dfrac{1}{u}$

This equation should be used in order to calculate the object distance. Substitute all the values given and get into an answer. Also don’t forget to apply sign convention. Then find the distance to the wall from the object.

Complete answer:
first of all let us draw the diagram indicating these details.
In this according to the question.

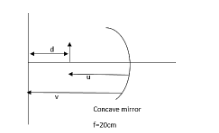
It has been asked to find out the distance to the object and the distance to the image as well as the focal length has been given. Therefore we can apply the mirror equation in order to solve this question.
According to the equation,
$\dfrac{1}{f}=\dfrac{1}{v}+\dfrac{1}{u}$
Where $f$ be the focal length, $u$ be the initial velocity and $v$be the final velocity.
In the question it is given that,
$f=-20cm$
$v=+50cm$
Substituting this values into the equation,
$\dfrac{1}{-20}=\dfrac{1}{-50}+\dfrac{1}{u}$
Rearranging the equation will give,

$\begin{aligned} & \dfrac{1}{u}=\dfrac{1}{20}-\dfrac{1}{50}=\dfrac{50-20}{50\times 20} \\\ & \implies u=\dfrac{30}{1000} \\\ & \implies u=\dfrac{100}{3}cm \\\ \end{aligned}$

That is the object should be placed to form its real image on the wall at a distance of $\dfrac{100}{3}cm$ from the mirror. And the distance from the mirror to the wall is already given in the question.
$v=50cm$

Taking the difference of both will give the total distance to the wall.
$\begin{aligned} & d=v-u \\\ & \implies d=50-\dfrac{100}{3} \\\ & \implies d=16.7cm \\\ \end{aligned}$
Hence the correct answer is $d=16.7cm$. Therefore the question is solved.

Note:
Concave mirrors are able to produce both real as well as virtual images. If the image is upright then it is virtual or if the image is inverted then it is real. They can also be enlarged, reduced, or have the same magnification of the body.