Question

A concave mirror of focal length 10 cm and a convex mirror of length 15 cm are placed facing each other 40 cm apart. A point object is placed between the mirrors, on their common axis and 15 cm from the concave mirror. Find the position and nature of the image produced by successive reflections, first at the concave mirror and then at the convex mirror.
A. 12 cm behind convex mirror, real
B. 9 cm behind convex mirror, real
C. 6 cm behind convex mirror, virtual
D. 3 cm behind convex mirror, virtual

Answer 1

If a hollow sphere is cut into parts and the outer surface of the cut part is painted, then it becomes a mirror with its inner surface as the reflecting surface. This kind of mirror is known as a concave mirror. Light converges at a point when it strikes and reflects back from the reflecting surface of the concave mirror. Hence, it is also known as a converging mirror.
If the other cut part of the hollow sphere is painted from inside, then its outer surface becomes the reflecting surface. This kind of mirror is known as a convex mirror. A convex mirror is also known as a diverging mirror as this mirror diverges light when they strike on its reflecting surface.

Complete step by step solution:
According to the question the diagram can be drawn as:

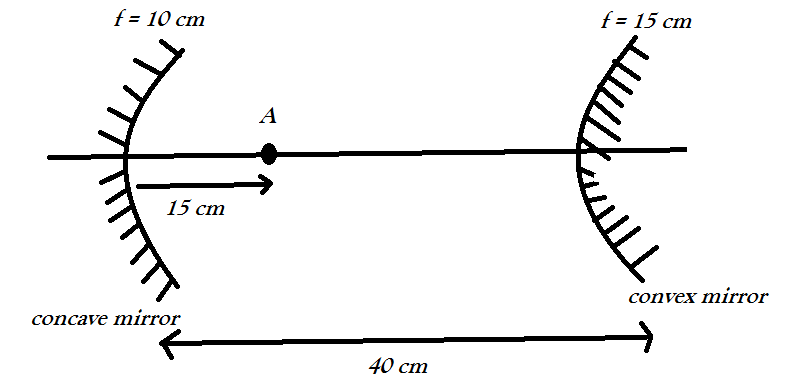
Here the point object A is placed at a distance of 15 cm in front of the concave mirror.
Then we have to find the position and nature of image after two successive reflections.
Therefore, now when the 1st reflection occurs on the concave mirror,
Then, we can write,

Position of object $(u) = - 15cm$
Focal length of the concave mirror $(f) = - 10cm$
Therefore from mirror formula we can calculate the position of image $(v)$ of the object
$\therefore this \Rightarrow \dfrac{1}{v} + \dfrac{1}{u} = \dfrac{1}{f} \\\ \Rightarrow \dfrac{1}{v} = \dfrac{1}{f} - \dfrac{1}{u} \\\ \Rightarrow \dfrac{1}{v} = \dfrac{1}{{ - 10}} - \dfrac{1}{{ - 15}} \\\ \Rightarrow \dfrac{1}{v} = - \dfrac{1}{{10}} + \dfrac{1}{{15}} \\\ \Rightarrow \dfrac{1}{v} = \dfrac{{ - 3 + 2}}{{30}} \\\ \Rightarrow \dfrac{1}{v} = \dfrac{{ - 1}}{{30}} \\\ \Rightarrow v = - 30cm \\\$
Therefore the 1st image is formed at 30 cm in front of the concave mirror.
Now, this image serves as the object for the convex mirror during the second reflection.

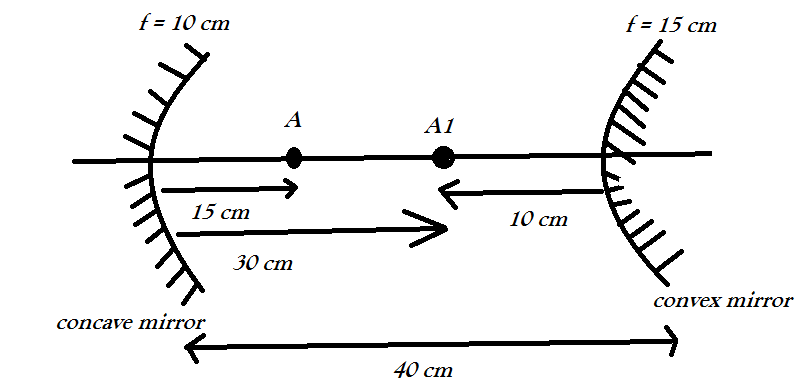
In other words A1 will serve as the object for the convex mirror.
Thus the updated values are:

Position of object $(u) = - 10cm$
Focal length of the convex mirror $(f) = + 15cm$
Therefore the position of image$(v)$:

$$\therefore this \Rightarrow \dfrac{1}{v} = \dfrac{1}{f} - \dfrac{1}{u} \\\ \Rightarrow \dfrac{1}{v} = \dfrac{1}{{ + 15}} - \dfrac{1}{{ - 10}} \\\ \Rightarrow \dfrac{1}{v} = \dfrac{1}{{15}} + \dfrac{1}{{10}} \\\ \Rightarrow \dfrac{1}{v} = \dfrac{5}{{30}} \\\ \Rightarrow \dfrac{1}{v} = \dfrac{1}{6} \\\ \Rightarrow v = 6cm \\\$$

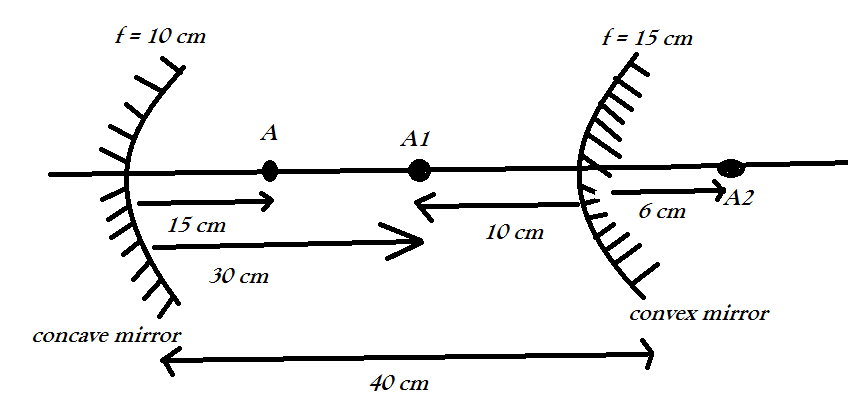
Since v is positive and u is negative so, the image will be virtual

Thus the image (A2) will be formed behind the convex mirror at a distance of 6 cm and will be virtual. Option C is the correct answer.

Note: While solving these types of questions always follow the sign convention carefully and always write the focal length of the corresponding mirrors with proper sign.