Question

A concave mirror is placed on a horizontal table, with its axis directed vertically upward. Let O be the pole of the mirror and C be the center of curvature. A point object is placed at C. It has a real image also, located at C. If the mirror is filled with water, the image will be
A. real, and it will remain at C.
B. real, and located at a point between C and $\infty$
C. virtual, and located at a point between C and O.
D. real, and located at a point between C and O.

Answer 1

The relationship between the distances of the image and object from the pole and the focal length of the mirror is given by an equation known as the Mirror Equation.
Mirror Equation:
$\dfrac{1}{u} + \dfrac{1}{v} = \dfrac{1}{f}$
$u$ is the distance of the object from the pole
$v$ is the distance of the image from the pole
$f$ is the focal length of the mirror
The image is said to be real if the image can be captured on a screen. It is always inverted and real images are always formed in front of the mirror.

Complete step by step solution:
The center of curvature of a mirror is defined as the center of the circle that the concave mirror was a part.

Here is the ray diagram of the image formation when the object is placed at the center of curvature.

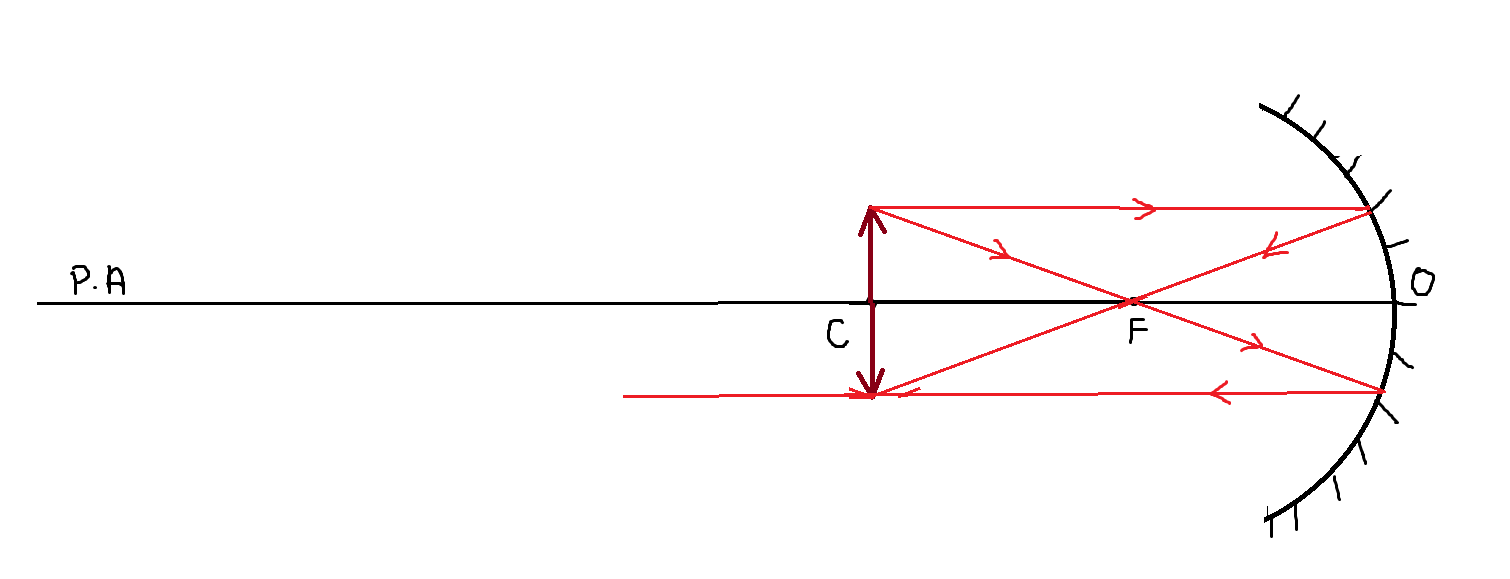
There are two rays emanating from the object.
- The first ray parallel to the principal axis, after reflection, passes through focus F.
- The second ray passing through focus, after reflection passes parallel to the principal axis.
The characteristics of the image formed are:
- The image is real since it is formed in front of the mirror and the image can be captured on the screen.
- The image is inverted.
- The image is of the same size.
- The image is formed at the centre of curvature.
The mirror equation is –
$\dfrac{1}{u} + \dfrac{1}{v} = \dfrac{1}{f}$
$f = \dfrac{R}{2}$
where
$R$ is the radius of curvature of the mirror
From the above equations, it is evident that the focal length is dependent only on the curvature of the mirror and it does not depend on the medium in which it is present. Hence, placing the entire apparatus inside the water will not result in any change in the position of the image.

$\therefore$ Thus, the image formed is real and formed at the center of curvature, C. Hence, the correct option is Option (A).

Note:
In most of the cases in a concave mirror, the images formed are real and inverted. However, this is true until the object is kept beyond the focal length, beyond which, the image becomes virtual and erect. Also, in all cases in a convex mirror, the image formed is virtual, erect, and diminished.
Thus, unless otherwise mentioned, we can assume that if we see a concave mirror in the question, we should be ready for a real image.