Question

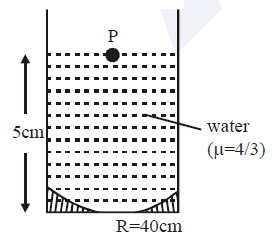
A concave mirror has a radius of curvature of 40cm. It is at the bottom of a glass that has water filled up to 5cm (see figure). If a small particle is floating on the surface of water, its image as seen, from directly above the glass, is at a distance ‘d’ from the surface of water. The value of d is close to: (Refractive index of water = 1.33)

A. 8.8 cm
B. 11.7 cm
C. 6.7 cm
D. 13.4 cm

Answer 1

Hint: As the object distance and radius of curvature is given, we shall use mirror formula to find the image distance and then, we will substitute the values in the object distance formula to get the value of ‘d’.
Formula used: $\dfrac { 1 }{ u } +\dfrac { 1 }{ v } =\dfrac { 1 }{ f }$

Complete step by step solution:
To calculate the image distance and height of an image due to reflection from the curved surface, a mirror formula is used. Which can be written as
$\dfrac { 1 }{ u } +\dfrac { 1 }{ v } =\dfrac { 1 }{ f }$
The light that is incident on the particle ‘p’ will be reflected at the mirror. From the question, we know u = -5 cm and $f=-\dfrac { R }{ 2 }$ which becomes f = -20 cm.
On substituting values of ‘f’ and ‘u’ in the mirror formula, we get
$\dfrac { 1 }{ -5 } +\dfrac { 1 }{ v } =\dfrac { 1 }{ -20 }$
$\dfrac { 1 }{ v } =+\dfrac { 1 }{ 5 } -\dfrac { 1 }{ 20 }$
On taking LCM and solving, it becomes
$\dfrac { 1 }{ v } =\dfrac { 3 }{ 20 }$
For the value of ‘v’, we should reciprocate it
$v=\dfrac { 20 }{ 3 }$
The image will act only as an object for light that is refracting at the water surface.
So, the object distance is calculated as ${{d}_{1}}=5+\dfrac{20}{3}=\dfrac{35}{3}cm$
Now considering below the surface of water, after refraction the final image is formed at ‘d’
Which can be calculated as $d={{d}_{1}}\dfrac{{{\mu }_{2}}}{{{\mu }_{1}}}$
Where, μ2 is the refractive index of medium
μ1 is the refractive index of water
Let us substitute the values in the equation to determine ‘d’
$d=\left( \dfrac { 35 }{ 3 } \right) \left( \dfrac { 1 }{ 1.33 } \right)$
On solving, we get
d = 8.77 cm, which can be rounded off as 8.8 cm
Therefore, the correct answer for the given question is option (A).

Note: The mirror formula holds for both the concave and convex mirrors, but the concave mirror has a positive focal length. For a concave mirror, if the object is placed within the focus, the image formed is virtual and it cannot be obtained on the screen.