Question

A concave lens forms the image of an object such that the distance between the object and image is 10 cm and the magnification produced is $\dfrac{1}{4}$. The focal length of the lens will be
A. 8.6 cm
B. 6.2 cm
C. 10 cm
D. 4.4 cm

Answer 1

The formula for calculating the magnification of the lens and the Lens formula should be used to solve this problem. Using the magnification of the lens formula, we will find the value of the object and image distance. Using the Lens formula, we will find the value of the focal length by substituting the values of the object and image distance obtained.

Formula used:

& m=\dfrac{v}{u} \\\ & \dfrac{1}{f}=\dfrac{1}{v}-\dfrac{1}{u} \\\ \end{aligned}$$ **Complete step-by-step answer:** The diagram of the lens arrangement. 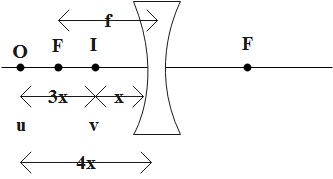 The formulae used are: The magnification formula is, $$m=\dfrac{v}{u}$$ Where v is the image distance and u is the object distance Lens formula $$\dfrac{1}{f}=\dfrac{1}{v}-\dfrac{1}{u}$$ Where f is the focal length From given, we have the data as follows: The distance between the object and image is 10 cm. $$\Rightarrow u-v=10\,cm$$ $$\Rightarrow v=u-10$$…… (1) The magnification produced by the lens is$$\dfrac{1}{4}$$. $$\Rightarrow \dfrac{v}{u}=\dfrac{1}{4}$$…… (2) Equate the equation (1) in (2), so, we get, $$\begin{aligned} & \dfrac{u-10}{u}=\dfrac{1}{4} \\\ & \Rightarrow 4u-40=u \\\ & \Rightarrow u=\dfrac{40}{3}cm \\\ \end{aligned}$$ Hence the object distance from the lens. Substitute the value of the object distance in one of the equations (1) or (2) to find the image distance. $$\begin{aligned} & \dfrac{v}{{}^{40}/{}_{3}}=\dfrac{1}{4} \\\ & \Rightarrow v=\dfrac{10}{3}cm \\\ \end{aligned}$$ Hence the image distance from the lens. Now, we will consider the Lens formula. $$\dfrac{1}{f}=\dfrac{1}{v}-\dfrac{1}{u}$$ Substitute the obtained values of the image and object distance. $$\begin{aligned} & \dfrac{1}{f}=\dfrac{1}{{}^{10}/{}_{3}}-\dfrac{1}{{}^{40}/{}_{3}} \\\ & \Rightarrow \dfrac{1}{f}=\dfrac{3}{10}-\dfrac{3}{40} \\\ \end{aligned}$$ Continue the further calculation. $$\begin{aligned} & \dfrac{1}{f}=\dfrac{9}{40} \\\ & \Rightarrow f=\dfrac{40}{9}cm \\\ \end{aligned}$$ Hence the value of the focal length of the lens. As the value of the focal length of the lens obtained is equal to $$\dfrac{40}{9}cm=4.4cm$$, thus, the option (D) is correct. **So, the correct answer is “Option (D)”.** **Note:** This is a direct question, as we have substituted the values in the formulae to obtain the value of the focal length of the lens. Even by giving the values of the focal length of the lens and one of two parameters, that is, the object distance or image distance, the other parameter can be asked.