Question

A compound rod has a steel core of diameter 1cm and an outer casing of copper whose outer diameter is 2cm. The length of this compound rod is ${\text{2m}}$ and one end is maintained at $100^\circ {\text{C}}$ while the other end is at $0^\circ {\text{C}}$. If the outer surface of the rod is thermally insulated, then find the heat current in the rod.
(Given: thermal conductivity of steel is $12{\text{cal}}{{\text{K}}^{ - 1}}{{\text{m}}^{ - 1}}{{\text{s}}^{ - 1}}$, thermal conductivity of copper is ${\text{92cal}}{{\text{K}}^{ - 1}}{{\text{m}}^{ - 1}}{{\text{s}}^{ - 1}}$ ).
A) ${\text{2cal}}{{\text{s}}^{ - 1}}$
B) ${\text{1}} \cdot {\text{13cal}}{{\text{s}}^{ - 1}}$
C) ${\text{1}} \cdot {\text{42cal}}{{\text{s}}^{ - 1}}$
D) ${\text{2}} \cdot {\text{68cal}}{{\text{s}}^{ - 1}}$

Answer 1

The amount of heat flowing through the inner core or the outer casing depends on the thermal conductivity of the material, its cross-sectional area, the temperature difference, and the length of the rod. The heat current in the rod refers to the rate at which heat flows through the compound rod. It will be the sum of the rate of flow through the steel core and that through the copper core.

Formulas used:
The amount of heat flowing through a rod kept at a temperature difference $\Delta T$ between its ends is given by, $Q = \dfrac{{\kappa \pi {r^2}\Delta T}}{l}$ where $\kappa$ is the thermal conductivity of the material of the rod, $\pi {r^2}$ is the cross-sectional area of the rod and $l$ is the length of the rod.

Complete step by step answer:
Step 1: Sketching a figure of the compound rod and list its parameters.
The given compound rod can be considered to be a rod within another rod. The figure given below depicts this arrangement.

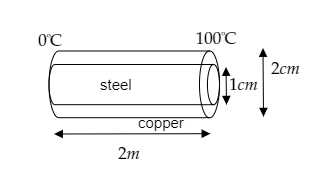
The inner rod is steel and its diameter is given to be ${d_s} = 1{\text{cm}}$ .
$\Rightarrow {r_s} = 0 \cdot 5{\text{cm}}$
The outer rod is copper and its outer diameter is given to be ${d_c} = 2{\text{cm}}$ .
$\Rightarrow {r_c} = 1{\text{cm}}$
The length of the rod is given to be $l = {\text{2m}}$ .
The temperature difference of the rod is $\Delta T = 100 - 0 = 100^\circ {\text{C}}$ .
Also, we have the thermal conductivity of steel as
$\Rightarrow {\kappa _s} = 12{\text{cal}}{{\text{K}}^{ - 1}}{{\text{m}}^{ - 1}}{{\text{s}}^{ - 1}}$ and that of copper as ${\kappa _c} = {\text{92cal}}{{\text{K}}^{ - 1}}{{\text{m}}^{ - 1}}{{\text{s}}^{ - 1}}$ .
Step 2: Expressing the heat flowing in the steel rod.
Now the amount of heat flowing through the inner rod is given by,
${Q_s} = \dfrac{{{\kappa _s}\pi {r_s}^2\Delta T}}{l}$ ------ (1)
Substituting for ${\kappa _s} = 12{\text{cal}}{{\text{K}}^{ - 1}}{{\text{m}}^{ - 1}}{{\text{s}}^{ - 1}}$, ${r_s} = 0 \cdot 5 \times {10^{ - 2}}{\text{m}}$, $l = {\text{2m}}$ and $\Delta T = 100{\text{K}}$ in equation (1) we get,
$\Rightarrow {Q_s} = \dfrac{{12\pi {{\left( {0 \cdot 5 \times {{10}^{ - 2}}} \right)}^2}100}}{2} = 0 \cdot 015\pi {\text{cal}}{{\text{s}}^{ - 1}}$
Thus the amount of heat flowing in the steel rod is
$\Rightarrow {Q_s} = 0 \cdot 015\pi {\text{cal}}{{\text{s}}^{ - 1}}$ .
Similarly, we have the amount of heat flowing in between the copper rod as
${Q_c} = \dfrac{{{\kappa _c}\pi \left( {{r_c}^2 - {r_s}^2} \right)\Delta T}}{l}$ ------ (2)
Substituting for ${\kappa _c} = 92{\text{cal}}{{\text{K}}^{ - 1}}{{\text{m}}^{ - 1}}{{\text{s}}^{ - 1}}$, ${r_c} = 1 \times {10^{ - 2}}{\text{m}}$, ${r_s} = 0 \cdot 5 \times {10^{ - 2}}{\text{m}}$, $l = {\text{2m}}$ and $\Delta T = 100{\text{K}}$ in equation (2) we get,
$\Rightarrow {Q_c} = \dfrac{{92\pi \left( {{1^2} - 0 \cdot {5^2}} \right) \times {{10}^{ - 4}}100}}{2} = 0 \cdot 345\pi {\text{cal}}{{\text{s}}^{ - 1}}$
Thus the amount of heat flowing in between the copper rod is ${Q_c} = 0 \cdot 345\pi {\text{cal}}{{\text{s}}^{ - 1}}$ .
Step 3: Expressing the heat current in the rod.
The heat current in the compound rod can be expressed as
$\dfrac{Q}{t} = \dfrac{{{Q_s}}}{t} + \dfrac{{{Q_c}}}{t}$
$\Rightarrow Q = {Q_s} + {Q_c}$ ---------- (3)
Substituting for ${Q_s} = 0 \cdot 015\pi {\text{cal}}{{\text{s}}^{ - 1}}$ and ${Q_c} = 0 \cdot 345\pi {\text{cal}}{{\text{s}}^{ - 1}}$ in equation (3) we get,
$\Rightarrow Q = 0 \cdot 015\pi + 0 \cdot 345\pi = 1 \cdot 13{\text{cal}}{{\text{s}}^{ - 1}}$

Thus the heat current in the rod will be ${\text{1}} \cdot {\text{13cal}}{{\text{s}}^{ - 1}}$. So the correct option is B.

Note:
While substituting values for the various physical quantities in equations (1) and (2), all the physical quantities must be expressed in their respective S.I. units. Here the radii of the steel core and the outer casing were expressed in centimeters, so while substituting these were converted into meters. Conversion of the temperature difference into the Kelvin scale is not necessary as the temperature difference in the Celsius scale will have the same value in the Kelvin scale.
In the Celsius scale, $\Delta T = 100 - 0 = 100^\circ {\text{C}}$ and in the Kelvin scale it will be $\Delta T = 373 - 273 = 100{\text{K}}$ .