Question

A compound of formula ${A_2}{B_3}$ has the hcp lattice. Which atom forms the hcp lattice and what fraction of tetrahedral voids is occupied by the other atoms?
(A) ${\text{hcp lattice - A, }}\dfrac{2}{3}{\text{ Tetrahedral voids - B}}$
(B) ${\text{hcp lattice - B, }}\dfrac{1}{3}{\text{ Tetrahedral voids - A}}$
(C) ${\text{hcp lattice - B, }}\dfrac{2}{3}{\text{ Tetrahedral voids - A}}$
(D) ${\text{hcp lattice - A, }}\dfrac{1}{3}{\text{ Tetrahedral voids - B}}$

Answer 1

Hint : The hcp structure of a unit cell has three types of atoms in three layers. There are twelve atoms at the corners of the hexagon. Three atoms are present in between the top and bottom face of the hexagon, in alternate vertical faces. These atoms are present inside the face so that they cannot be shared by other cells.

Complete Step By Step Answer:
the structure of hcp unit cell is shown below:

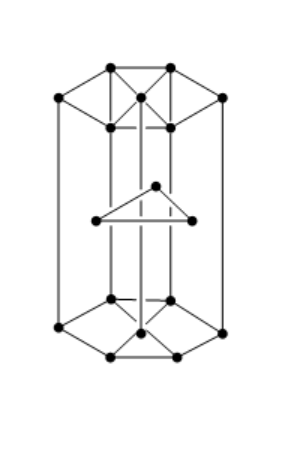
Let us consider that $B$ will produce the hcp lattice.
Total number of atoms in $B = 6$
Tetrahedral void occupied $= 2N$
So, $N = 6$
Tetrahedral void= $2 \times 6 = 12$
Now, the number of atoms in A $= \dfrac{1}{3} \times {\text{Tetrahedral void}}$
$= \dfrac{1}{3} \times 12$
$= 4$
So, the compound will be ${A_4}{B_6}$ which can be simplified and written as ${A_2}{B_3}$
Therefore, option B is the correct answer.

Note :
The closest packing of spheres in two dimensions has a hexagonal symmetry in which every sphere has six nearest neighbors. In hcp, each atom has twelve nearest neighbours. Consider an ideal structure, then the distance between the planes is $1.633a$ , where $a$ is the distance between the atoms of the unit cell.