Question

A compound ${M_p}{X_q}$ has cubic-close packing (c.c.p) arrangement of X. Its unit-cell structure is shown below. The empirical formula of the compound is:

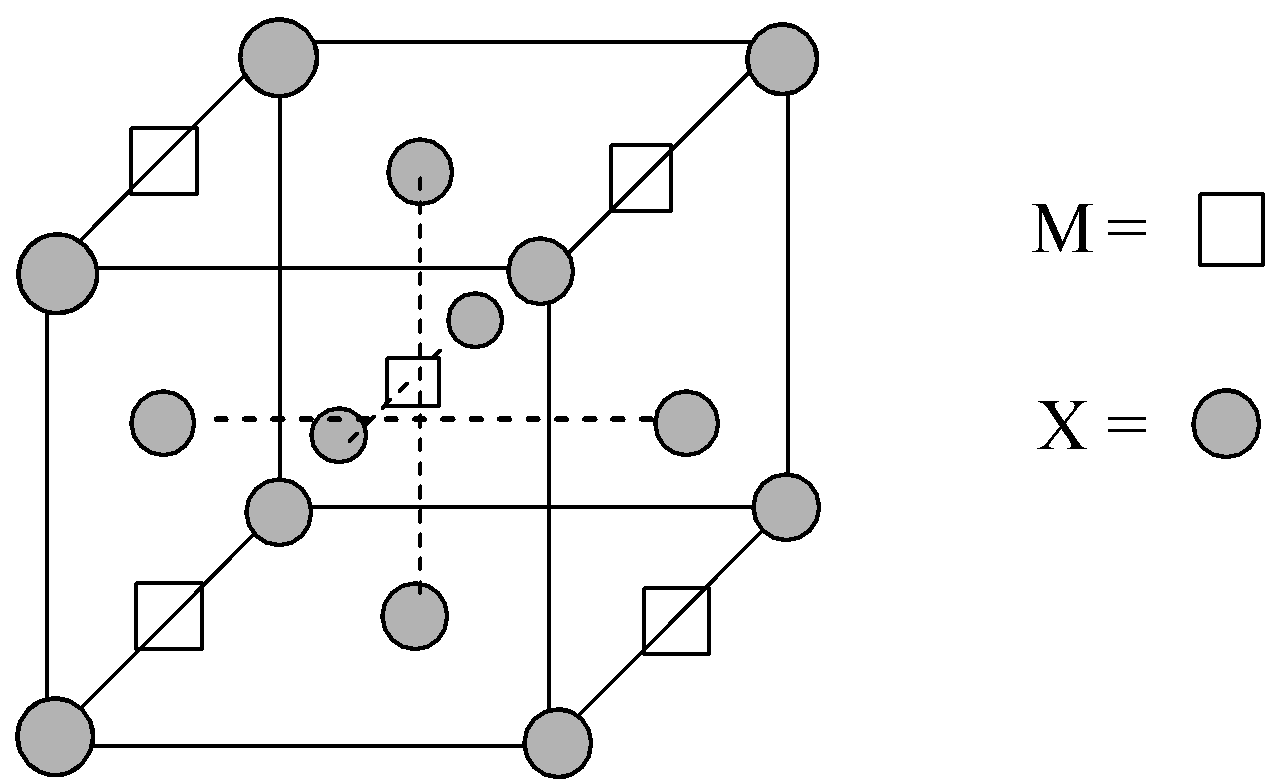
A) $MX$
B) $M{X_2}$
C) ${M_2}X$
D) ${M_5}{X_{14}}$

Answer 1

Count the number of M atoms and X atoms at different positions in the given structure of the unit-cell. To answer this question, you should know the contribution of an atom per unit cell, when the atoms are located at the corners, face-centre, and the edge-centre.

Complete step by step answer:
Given structure of the unit cell of the compound ${M_p}{X_q}$:

Now, let us understand the positions of X atoms:
Number of X atoms located at the corners = 8,
Number of X atoms located at the face-centres = 6
And, contribution of an atom located at the corner in a unit cell = $\dfrac{1}{8}$ per unit cell.
Contribution of an atom located at the face-centre in a unit cell = $\dfrac{1}{2}$ per unit cell.
Thus, total number of X atoms in the unit cell = ${\text{8 corner atoms }} \times \dfrac{1}{8}{\text{ atom per unit cell + 6 face - centred atoms }} \times {\text{ }}\dfrac{1}{2}{\text{ atom per unit cell }}$
$\therefore$ Total number of X atoms = $1 + 3 = 4{\text{ atoms}}$

Now, there are four M atoms located at the edge-centres and one atom is located at the body centre of the unit cell.
Contribution of an atom located at the edge centre in a unit-cell = $\dfrac{1}{4}$ per unit cell.
Contribution of an atom located at the body-centre in a unit-cell = 1 per unit cell.
Thus, total number of M atoms in the unit cell = ${\text{4 edge - centred atoms }} \times {\text{ }}\dfrac{1}{4}{\text{ atom per unit cell + 1 body - centred atom }} \times {\text{ 1 atom per unit cell}}$
$\therefore$ Total number of M atoms = $1 + 1 = 2{\text{ atoms}}$
So, there are a total two M atoms and four X atoms in the given unit cell structure. Thus, the empirical formula of the compound is ${M_2}{X_4}$ or on simplifying, $M{X_2}$.
So, the correct answer is “Option B”.

Note: Cubic close packed (ccp) unit cell or face-centred cubic (fcc) unit cell are the same unit cells but two different names. A face-centred unit cell contains atoms at all the corners and at the centre of all the faces of the cubic unit cell. A key point to note is that each atom located at the face centre is shared between two adjacent unit cells and hence only $\dfrac{1}{2}$ of each atom belongs to the unit cell.