Question
Question: A compound \( {M_p}{X_q} \) has cubic close packing \( (ccp) \) arrangement of X. Its unit cell stru...
A compound MpXq has cubic close packing (ccp) arrangement of X. Its unit cell structure is shown below. The empirical formula of the compound is:
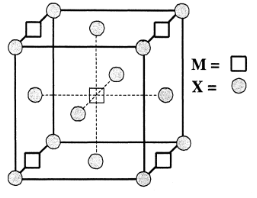
(A) MX
(B) MX2
(C) M2X
Solution
Hint : A CCP arrangement has a total of 4 spheres per unit cell and an HCP arrangement has 8 spheres per unit cell. However, both configurations have a coordination number of 12.
The packing efficiency is the fraction of volume in a crystal structure that is occupied by constituent particles, rather than empty space. In order to find this, the volume of the spheres needs to be divided by the total volume (including empty spaces) occupied by the packed spheres.
Complete Step By Step Answer:
If this arrangement has ccp packing then no. of atom of X will be as follows:
The contribution of one corner atom in the unit cell is: 81 atom
So the contribution of all 8 corner atom will be: 81×8=1atom
Now the contribution of X type atom of the face of cell
The contribution of one face atom in the unit cell is: 21atom
So the contribution of all 6 face atom will be: 21×6=3atoms
Now total number of X atoms will be: 1+3=4atoms
Now number of M type atoms-
The contribution of one atom on edge is: 41
So the contribution of 4 edge atoms will be: 41×4=1atom
Now the contribution of M type atom in the center of unit cell: 1atom
Total number of M type atom will be: 1+1=2atoms
So, the unit cell formula for the compound will be M2X4 and the empirical formula will be MX2 which is our A option.
Note :
The arrangement of the atoms in a crystalline solid affects atomic coordination numbers, interatomic distances, and the types and strengths of bonding that occur within the solid. An understanding of atomic packing in a unit cell and crystal lattice can give insight into the physical, chemical, electrical, and mechanical properties of a given crystalline material.
