Question

A composite resistance of $50\Omega$ which can carry a current of 4 A is to be made from resistances each of resistance $100 \Omega$ which can carry a current of 1A. The minimum number of resistances to be used is:
A.4
B.8
C.12
D.16

Answer 1

Here, the composite resistance means equivalent resistance. So, the equivalent resistance of the number of resistances used should be equal to $50\Omega$. Check, the options if any of them give the equivalent resistance to be $50\Omega$, These resistors will be connected in parallel as the equivalent resistance is less than the resistance of an individual resistor. The option that will give the equivalent resistance to be $50\Omega$ that much number of resistances is to be used.
Formula used:
$\dfrac {1}{{R}_{eq}}= \dfrac {1} {{R}_{1}} + \dfrac {1}{{R}_{2}}+ \dfrac {1}{{R}_{3}}+ …+\dfrac {1}{{R}_{N}}$

Complete answer:
Given: Composite resistance = $50\Omega$
Current through $50\Omega$ = 4 A
Value of each resistance = $100 \Omega$
Current through each $100 \Omega$ resistor= 1 A
Equivalent resistance is given by,
$\dfrac {1}{{R}_{eq}}= \dfrac {1} {{R}_{1}} + \dfrac {1}{{R}_{2}}+ \dfrac {1}{{R}_{3}}+ …+\dfrac {1}{{R}_{N}}$
If we consider 4 pairs of resistances connected in parallel. The value of each pair will be $200 \Omega$.

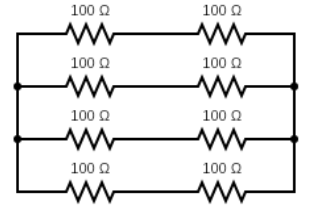
Then the equivalent resistance will be,
$\dfrac {1}{{R}_{eq}}= \dfrac {1} {{R}_{1}} + \dfrac {1}{{R}_{2}}+ \dfrac {1}{{R}_{3}}+ \dfrac {1}{{R}_{4}}$
Substituting the values in above equation we get,
$\dfrac {1}{{R}_{eq}}= \dfrac {1}{200}+\dfrac {1}{200}++\dfrac {1}{200}++\dfrac {1}{200}$
$\Rightarrow \dfrac {1}{{R}_{eq}}= \dfrac {4}{200}$
$\Rightarrow {R}_{eq}= \dfrac {200}{4}$
$\Rightarrow {R}_{eq}= 50 \Omega$
Now, as the resistances are connected in parallel. The total current entering the system will be equal to the current leaving the system. Thus, the total current flowing through these 8 resistors will be 4 A.
Hence, the minimum number of resistances to be used is 8.

So, the correct answer is option B i.e. 8.

Note:
Students should remember that the equivalent resistance of a combination is always less than the smallest resistance in the parallel network. As we add more resistors in the network, the total resistance of the circuit will always decrease. While, in a series network, the equivalent resistance of the network is greater than the value of the largest resistor in the chain. The current flowing through each parallel branch may not be the same. But the voltage across each resistor in a parallel network is always the same.