Question

A Composite block is made up of slabs A, B, C, D and E of different thermal conductivities (given in terms of constant K) and sizes (given in terms of length L) as shown in figure. All slabs are of the same width. Heat Q flows from left to right through the blocks. Then in a steady state

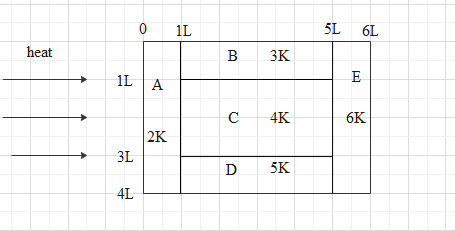
(This question has multiple correct options.)
A) Heat flow through the slabs A and E are the same.
B) Heat flow through slab E is maximum.
C) Temperature difference across slab E is smallest.
D) Heat flow through C= heat flow through B + heat flow through D

Answer 1

Here we have given a system, through which heat is flowing from left to right and we have to find, in steady state which of the given statements is/are right. For that we will use the formula of heat flow and thermal resistivity to check which option/options is/are right.

Formula used:

& R=\dfrac{l}{KA} \\\ & Q=\dfrac{\Delta T}{R} \\\ \end{aligned}$$ **Complete step by step answer:** We have to find the answer for the question in steady state i.e. when the amount of heat entering a system will be equal to the amount of heat existing in the system. As heat is flowing from left to right, then the flow of heat through slab can be shown as  So the heat which is entering in slab A divides into 3 parts and flows into B, C, and D and then from B, C and D the heat is flowing into E and then it exits the system. We can say that heat is entering from slab A and existing from slab E. Hence heat flowing through A will be equal to heat flowing through E. So option A is right and B is wrong as heat flow through E can’t be maximum as it is equal to heat flow through A. Now the next statement (option C) is about temperature difference and temperature difference is proportional to thermal resistance. Thermal resistance is be given as $$R=\dfrac{l}{KA}$$ Where l is length, K is thermal conductivity and A is the area. We know the value of length, thermal conductivity and breadth is also given for each slab so we can calculate area hence thermal resistivity for each slab. So thermal resistivity of slab A will be $$\begin{aligned} & {{R}_{A}}=\dfrac{L}{\left( 2K \right)\left( L\times 4L \right)} \\\ & \Rightarrow {{R}_{A}}=\dfrac{L}{8K{{L}^{2}}} \\\ & \Rightarrow {{R}_{A}}=\dfrac{1}{8KL} \\\ \end{aligned}$$ Similarly, thermal resistivity of slab B will be $$\begin{aligned} & {{R}_{B}}=\dfrac{4L}{\left( 3K \right)\left( 4L\times L \right)} \\\ & \Rightarrow {{R}_{B}}=\dfrac{4L}{12K{{L}^{2}}} \\\ & \Rightarrow {{R}_{B}}=\dfrac{1}{3KL} \\\ \end{aligned}$$ Similarly, calculating thermal resistivity of slab C, D and E gives us $${{R}_{C}}=\dfrac{1}{8KL},{{R}_{D}}=\dfrac{1}{5KL}\text{ and }{{R}_{E}}=\dfrac{1}{24KL}$$ Comparing values of thermal resistivity for each slab, the smallest value is for the slab E which is $$\dfrac{1}{24KL}$$. Hence option C is correct. Now the last statement is about heat flow . Heat flowing from C will be equal to sum of heat flow from B and D. So let us calculate the heat flow for slab B, C and D. Heat flow can be given as the ratio of temperature to resistivity. $$Q=\dfrac{\Delta T}{R}$$ Now we have already calculated the thermal resistivity of slabs so we can use those values to find the heat flow. Heat flow through slab B will be $$\begin{aligned} & {{Q}_{B}}=\dfrac{\Delta {{T}_{B}}}{{{R}_{B}}} \\\ & \Rightarrow {{Q}_{B}}=\dfrac{\Delta {{T}_{B}}}{\dfrac{1}{3KL}} \\\ & \Rightarrow {{Q}_{B}}=3KL\Delta {{T}_{B}} \\\ \end{aligned}$$ Similarly, calculating for slab C and D we get $${{Q}_{C}}=8KL\Delta {{T}_{C}}\text{ and }{{Q}_{D}}=5KL\Delta {{T}_{D}}$$ Now as heat is flowing from left to right therefore temperature across slab B, C, and D will be the same as shown in above temperature as it is in steady state. So heat flow through slab B, C and D will be given as $$\begin{aligned} & {{Q}_{B}}=3KL\Delta {{T}_{2}} \\\ & {{Q}_{C}}=8KL\Delta {{T}_{2}} \\\ & {{Q}_{D}}=5KL\Delta {{T}_{2}} \\\ \end{aligned}$$ Now sum of heat flow through B and D, is given as $$\begin{aligned} & {{Q}_{B}}+{{Q}_{D}}=3KL\Delta {{T}_{2}}+5KL\Delta {{T}_{2}} \\\ & \Rightarrow {{Q}_{B}}+{{Q}_{D}}=8KL\Delta {{T}_{2}} \\\ & \Rightarrow {{Q}_{B}}+{{Q}_{D}}={{Q}_{C}} \\\ \end{aligned}$$ **So, the correct answers are “Option A, C and D”.** **Note:** Given question is multiple correct option therefore it can have one or more than one correct option. Here 3 of them are correct. Temperature difference between B, C and D is the same as it is in steady state therefore temperature across the slab ends will remain constant because ends of slab B, C, and D are connected to slab A and E respectively.