Question

A complex of the type ${\left[ {M{{\left( {AA} \right)}_2}{X_2}} \right]^{n + }}$ is known to be optically active. What does this indicate about the structure of the complex? Give one example of such a complex.

Answer 1

In order to answer the question let us first understand what optically active means. The capacity to rotate the plane of polarisation of a linearly polarised light is known as optical activity. This effect can only be seen in chiral materials, which lack mirror symmetry.

Complete answer:
When a molecule is chiral, it is the cause of its optical activity. The property demonstrated by substances in which the plane of polarisation is rotated for plane-polarized light is known as optical activity.
An optically active complex of the type ${\left[ {M{{\left( {AA} \right)}_2}{X_2}} \right]^{n + }}$ indicates cis-octahedral structure, e.g., $cis - {\left[ {\operatorname{P} t{{\left( {en} \right)}_2}C{l_2}} \right]^{2 + }}$ or $cis - {[Cr{(en)_2}C{l_2}]^ + }$ because the mirror image isomers aren't superimposable.

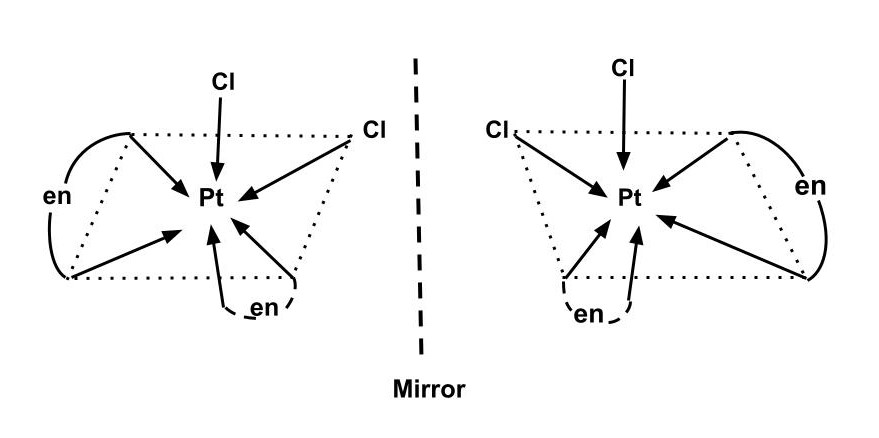
Additional Information:
In chemistry, the words dextrorotation and laevorotation (sometimes spelled levorotation) are used to describe the optical rotation of plane-polarized light. Dextrorotation refers to clockwise or right-handed rotation from the observer's perspective, while laevorotation refers to counter clockwise or left-handed rotation.

Note:
It should be known that Dextrorotatory or dextrorotatory refers to a chemical compound that causes dextrorotation, whereas laevorotatory or laevorotatory refers to a chemical component that causes laevorotation. Compounds with these features are said to have optical activity since they are made up of chiral molecules.] A chiral molecule's enantiomer (geometric mirror image) will be laevorotatory if it is dextrorotatory, and vice versa. Enantiomers rotate plane-polarized light in opposite directions by the same amount of degrees.