Question

A complex number $z$ is rotated in anticlockwise direction by an angle $a$ and we get ${z}'$, and if the same complex number $z$ is rotated by and angle $a$ in clockwise direction and we get ${z}''$, then
(a) ${z}',\text{ }z,\text{ }{z}''$ are in G.P.
(b) ${z}',\text{ }z,\text{ }{z}''$are in H.P.
(c) ${z}'+{z}''=2z\cos a$
(d) ${{\left( {{z}'} \right)}^{2}}+{{\left( {{z}''} \right)}^{2}}=2{{z}^{2}}\cos 2a$

Answer 1

First, we should know the condition that if a complex number $z$ is rotated by an angle $a$ in the anticlockwise direction, then we get the answer to be $z{{e}^{ia}}$. Then, we should know the condition that if a complex number $z$ is rotated by an angle $a$ in the clockwise direction, then we get the answer to be $z{{e}^{-ia}}$. Then, by using these conditions, we can get the desired results.

Complete step-by-step solution:
In this question, we are supposed to find the conditions for the complex number $z=A+iB$ when it is rotated anticlockwise and clockwise as the diagram of the complex number is as:

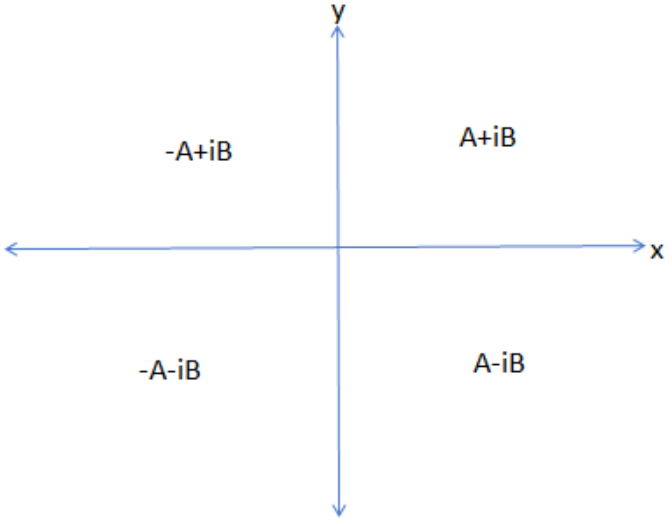
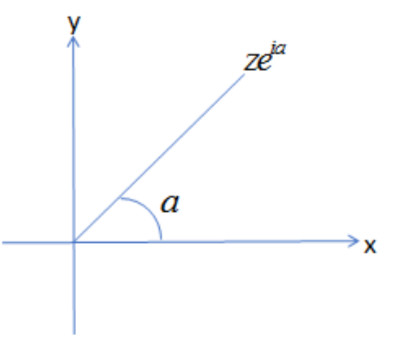
So, we should know the condition that if a complex number $z$ is rotated by an angle $a$ in the anticlockwise direction, then we get the answer to be $z{{e}^{ia}}$.

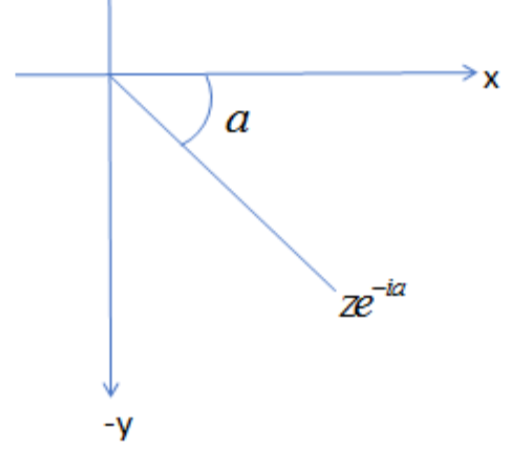
Similarly, we should know the condition that if a complex number $z$ is rotated by an angle $a$in the clockwise direction, then we get the answer to be $z{{e}^{-ia}}$.

So, in the above question, it is stated that when a complex number $z$ is rotated by an angle $a$ in the anticlockwise direction, then it is termed as ${z}'$.
So, it gives the result as:
${z}'=z{{e}^{ia}}.....\left( i \right)$
Similarly, in the above question it is stated that when a complex number $z$ is rotated by an angle $a$ in the clockwise direction, then it is termed as ${z}''$.
So, it gives the result as:
${z}''=z{{e}^{-ia}}......\left( ii \right)$
Now, if we multiply the above two equations (i) and (ii), we get:
$\begin{aligned} & {z}'{z}''=z{{e}^{ia}}\times z{{e}^{-ia}} \\\ & \Rightarrow {z}'{z}''={{z}^{2}}{{e}^{ia-ia}} \\\ & \Rightarrow {z}'{z}''={{z}^{2}}......\left( iii \right) \\\ \end{aligned}$
Now, by adding the equation (i) and (ii), we get:
$\begin{aligned} & {z}'+{z}''=z{{e}^{ia}}+z{{e}^{-ia}} \\\ & \Rightarrow {z}'+{z}''=z\left( {{e}^{ia}}+{{e}^{-ia}} \right) \\\ & \Rightarrow {z}'+{z}''=z\left( \cos a+i\sin a+\cos a-i\sin a \right) \\\ & \Rightarrow {z}'+{z}''=2z\cos a......\left( iv \right) \\\ \end{aligned}$
Now, by squaring the equation (i) and (ii) and then adding, we get:
$\begin{aligned} & {{\left( {{z}'} \right)}^{2}}+{{\left( {{z}''} \right)}^{2}}={{z}^{2}}{{e}^{2ia}}+{{z}^{2}}{{e}^{-2ia}} \\\ & \Rightarrow {{\left( {{z}'} \right)}^{2}}+{{\left( {{z}''} \right)}^{2}}={{z}^{2}}\left( {{e}^{2ia}}+{{e}^{-2ia}} \right) \\\ & \Rightarrow {{\left( {{z}'} \right)}^{2}}+{{\left( {{z}''} \right)}^{2}}={{z}^{2}}\left( \cos 2a+i\sin 2a+\cos 2a-i\sin 2a \right) \\\ & \Rightarrow {{\left( {{z}'} \right)}^{2}}+{{\left( {{z}''} \right)}^{2}}=2{{z}^{2}}\cos 2a....\left( v \right) \\\ \end{aligned}$
So, equation (iii) gives that ${z}',\text{ }z,\text{ }{z}''$ are in G.P.
Then, equation (iv) gives that ${z}'+{z}''=2z\cos a$.
Then, equation (v) gives that ${{\left( {{z}'} \right)}^{2}}+{{\left( {{z}''} \right)}^{2}}=2{{z}^{2}}\cos 2a$.
Hence, option (a), (c) and (d) all three are correct.

Note: The only mistake we can occur in these types of the questions is that we select the single answer as correct and tick mark it but the fact is that there are multiple answers correct in this question. So, in this type of question, we must be very careful before selecting our final answer.