Question

(a) Complete the following ray diagram:

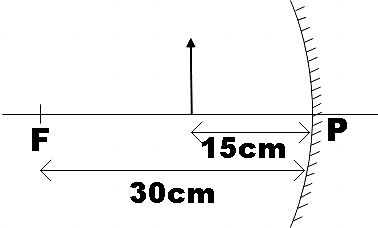
(b) Find the nature, position and size of the image formed.
(C) Use a mirror formula to determine the magnification in this case.

Answer 1

You could form the image of the object that is kept in between the focal point and pole of the mirror and thereby complete the given diagram. After completion you will understand the nature of the image so formed and you could use the mirror formula to find the position. Then you could use the expression for magnification to find the magnification in the given case.
Formula used:
Mirror formula,
$\dfrac{1}{f}=\dfrac{1}{v}+\dfrac{1}{u}$
Magnification,
$m=-\dfrac{v}{u}$

Complete answer:
(a) Here, we are asked to complete the given ray diagram.

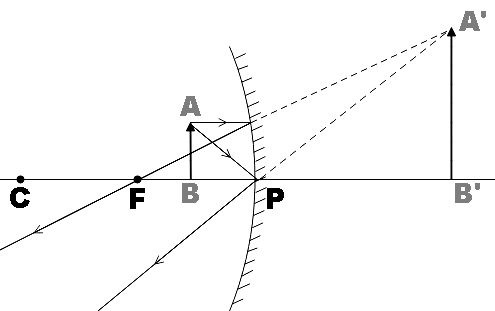
(b) Here, we are asked to find the nature, position and size of the image formed.
From the figure, we see that the object is kept in between the focal point and pole of the given concave mirror. On forming the image using certain steps that we normally follow, we find that the image is enlarged when compared to the object. Also, the image formed behind the mirror, so we could call an image so formed virtual. Also, we see that image formed is erect.
Now, let us recall the mirror formula given by,
$\dfrac{1}{f}=\dfrac{1}{v}+\dfrac{1}{u}$
$\Rightarrow v=\dfrac{uf}{u-f}$
$\Rightarrow v=\dfrac{-15\times -30}{-15+30}=\dfrac{450}{15}$
$\therefore v=30cm$
So, the image of the object kept between Pole (P) and focal point (F) will be virtual, erect and enlarged and will be formed 30cm behind the mirror.
(c) Now, let us recall the expression for magnification given by,
$m=-\dfrac{v}{u}$
$\Rightarrow m=-\dfrac{30}{\left( -15 \right)}$
$\therefore m=2$
Therefore, we found the magnification in the given case to be 2.

Note:
We have completed the ray diagram given in the question by using just two points. The ray that is parallel to the principal axis will pass through the focal point of the mirror after reflection. Then, we have the ray from the object incident at the pole of the mirror that makes equal angles after reflection.