Question

A company manufactures two types of toys A and B. A toy type of A requires 5 minutes for cutting and 10 minutes for assembling. A toy type of B requires 8 minutes for cutting and 8 minutes for assembling. There are 3 hours available for cutting and 4 hours for assembling the toy in a day. The profit is Rs. 50 each on a toy type of A and Rs.60 each on a toy of type B. How many toys of each type should the company manufacture in a day to maximize the profit? Use linear programming to find the solution.

Answer 1

We here need to find the number of toys of type A and B which maximize the profit every day. For this, we will first assume them to be x and y respectively and create an objective function which will give us the profit per day in terms of x and y. Then from the given conditions, we will form inequalities, which will act as constraints to this function. Then we will draw a graph of those inequalities and shade the region common to all. After doing that, we will note down the corner points of that region and check them one by one in our objective function. The coordinate of the point which will give the maximum value of the objective function will be our required point and will give us the value of x and y.

Complete step-by-step solution:
Here, we need to find the number of toys of type A and B so that the profit is maximum on each day.
For this, let us assume that the number of toys of type A is ‘x’ and that of type B is ‘y’.
Thus, we need to find the value of x and y.
Now, we have been given that profit on each type A toy, there is a profit of Rs.50. Thus, the total profit of x type A-toys will be:
$\begin{aligned} & 50\times x \\\ & \Rightarrow 50x \\\ \end{aligned}$
Similarly, we have been given that profit on each type B toy, there is a profit of Rs.60. Thus, the total profit of y type B toys will be:
$\begin{aligned} & 60\times y \\\ & \Rightarrow 60y \\\ \end{aligned}$
Thus, the total profit on both type A and type B toys will be:
$50x+60y$
We need to minimize it by linear programming and hence, it will be our objective function.
Thus, we can say that:
$Z=50x+60y$
Hence, we need to maximize Z.
Now, we have been given that it takes 5 minutes for cutting toys of type A and 8 minutes for cutting toys of type B.
Hence, the total time that will be taken for cutting x type A toys and y type B toys is given as:
$\begin{aligned} & 5\times x+8\times y \\\ & \Rightarrow 5x+8y \\\ \end{aligned}$
Now, we also have been given that the total time available for cutting toys in a day is 3 hours which is equal to $60\times 3=180$ minutes.
Thus, 180 will be the maximum value for the total time that will be taken for cutting x type A toys and y type B toys.
Thus, we can say that:
$5x+8y\le 180$
Now, we also have been given that it takes 10 minutes for assembling toys of type A and 8 minutes for cutting toys of type B.
Hence, the total time that will be taken for assembling x type A toys and y type B toys is given as:
$\begin{aligned} & 10\times x+8\times y \\\ & \Rightarrow 10x+8y \\\ \end{aligned}$
Now, we also have been given that the total time available for assembling toys in a day is 4 hours which is equal to $4\times 60=240$.
Thus, 240 will be the maximum value for the total time that will be taken for assembling x type A toys and y type B toys.
Thus, we can say that:
$10x+8y\le 240$
Now, since x and y are the number of type A and type B toys, their value will always be either greater than or equal to 0.
Thus, we can say that:
$\begin{aligned} & x\ge 0 \\\ & y\ge 0 \\\ \end{aligned}$
Now, these inequalities obtained are the conditions, which will be applied to maximize Z. Thus, we can say that these 4 inequalities will be the constraints to our objective function Z.
Thus, we will draw a graph of these 4 inequalities and shade the region common to all of them and check the corner points of that region to see which of them maximize Z.
Now, the first constraint is given as:
$5x+8y \le 180$
Thus, its corresponding equation will be:
$5x+8y=180$
Now, we will find two solutions to this equation.
Case-1: Let x= 0
Thus, putting x=0 in this equation we get:
$\begin{aligned} & 5x+8y=180 \\\ & \Rightarrow 5\left( 0 \right)+8y=180 \\\ & \Rightarrow 8y=180 \\\ & \Rightarrow y=\dfrac{180}{8}=\dfrac{45}{2} \\\ \end{aligned}$
Thus, the first solution to this equation is $\left( 0,\dfrac{45}{2} \right)$
Case-2: let y=0
Thus, putting y=0 in this equation we get:
$\begin{aligned} & 5x+8y=180 \\\ & \Rightarrow 5x+8\left( 0 \right)=180 \\\ & \Rightarrow 5x=180 \\\ & \Rightarrow x=\dfrac{180}{5}=36 \\\ \end{aligned}$
Thus, the second solution to this equation is (36,0).
Hence, the two solutions to this equation are $\left( 0,\dfrac{45}{2} \right)$ and (36,0).
Now, to see which side of this line is the required region, we will put (0,0) in this inequality and if it turns out to be correct, the side on which this point lies will be the required region otherwise it will be the other side.
Thus, putting (0,0) in this inequality we get:
$\begin{aligned} & 5x+8y\le 180 \\\ & \Rightarrow 5\left( 0 \right)+8\left( 0 \right)\le 180 \\\ & \Rightarrow 0+0\le 180 \\\ & \Rightarrow 0\le 180 \\\ \end{aligned}$
This inequality is correct, hence the side at which this point lies is the required side.
Now, the second constraint is given as:
$10x+8y\le 240$
Hence, its corresponding equation will be:
$10x+8y=240$
Now, we will find two solutions to it.
Case-1: let x=0
Thus, putting x=0 into this equation we get:
$\begin{aligned} & 10x+8y=240 \\\ & \Rightarrow 10\left( 0 \right)+8y=240 \\\ & \Rightarrow 8y=240 \\\ & \Rightarrow y=\dfrac{240}{8}=30 \\\ \end{aligned}$
Thus, the first solution to this equation is (0,30) .
Case-2: let y=0
Thus, putting y=0 into this equation we get:
$\begin{aligned} & 10x+8y=240 \\\ & \Rightarrow 10x+8\left( 0 \right)=240 \\\ & \Rightarrow 10x=240 \\\ \end{aligned}$
$\Rightarrow x=\dfrac{240}{10}=24$
Thus, the second solution to this equation will be (24,0).
Hence, the two solutions to this equation are (0,30) and (24,0).
Now, as we checked above, we will check (0,0) in this constraint too to find which side of the line is the required side.
Thus, putting (0,0) in this inequality we get:
$\begin{aligned} & 10x+8y\le 240 \\\ & 10\left( 0 \right)+8\left( 0 \right)\le 240 \\\ & 0+0\le 240 \\\ & 0\le 240 \\\ \end{aligned}$
This inequality is correct. Hence, the side of the line on which (0,0) will lie will be the required side.
Now, the next two constraints are:
$\begin{aligned} & x\ge 0 \\\ & y\ge 0 \\\ \end{aligned}$
Now, we know that these two inequalities represent the first quadrant.
Hence, from all these observations, we get the graph as:

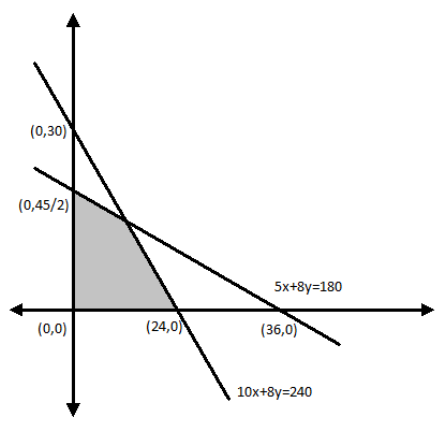
Now, we can see from the graph that these two lines intersect at a point which will also be one of the corner points.
We can find that point of intersection using the elimination method for the equations of these two inequalities.
Using the elimination method in the equations $5x+8y=180$ and $10x+8y=240$ we get:
$\begin{aligned} & \text{ }10x+8y=240 \\\ & \underline{-\left( 5x+8y=180 \right)} \\\ & \underline{\text{ }5x=60\text{ }} \\\ \end{aligned}$
Solving this, we will get:
$\begin{aligned} & 5x=60 \\\ & \Rightarrow x=\dfrac{60}{5}=12 \\\ \end{aligned}$
Now, by putting this value of x in any of these equations we will get the required value of y.
Hence, putting x=12 in the equation $10x+8y=240$we get:
$\begin{aligned} & 10x+8y=240 \\\ & \Rightarrow 10\left( 12 \right)+8y=240 \\\ & \Rightarrow 120+8y=240 \\\ & \Rightarrow 8y=120 \\\ & \Rightarrow y=\dfrac{120}{8}=15 \\\ \end{aligned}$
Hence, the required point is (12,15).
Thus, our graph will be:

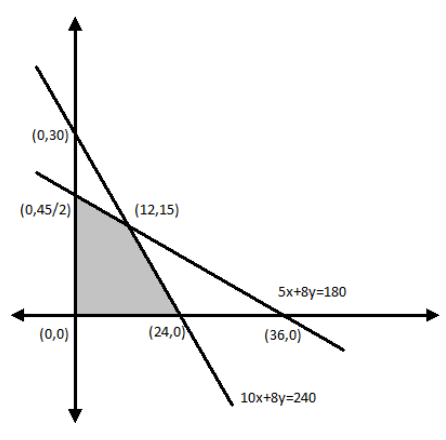
Now, we can see from the graph that the corner points of the shaded region are (0,0), (24,0), (12,15) and $\left( 0,\dfrac{45}{2} \right)$ .
Now, we will put these points one by one in Z and see which of them will maximize Z.
Now, putting (0,0) in Z we get:

& Z=50x+60y \\\ & \Rightarrow Z=50\left( 0 \right)+60\left( 0 \right) \\\ & \Rightarrow Z=0 \\\ \end{aligned}$$ Thus, we get Z=0 by (0,0). .....(i) Now, putting (24,0) in Z we get: $$\begin{aligned} & Z=50x+60y \\\ & Z=50\left( 24 \right)+60\left( 0 \right) \\\ & Z=1200+0 \\\ & Z=1200 \\\ \end{aligned}$$ Thus, we get Z=1200 by (24,0). .....(ii) Now, putting (12,15) in Z we get: $\begin{aligned} & Z=50z+60y \\\ & \Rightarrow Z=50\left( 12 \right)+60\left( 15 \right) \\\ & \Rightarrow Z=600+900 \\\ & \Rightarrow Z=1500 \\\ \end{aligned}$ Thus, we get Z=1500 by (12,15). .....(iii) Now, $\left( 0,\dfrac{45}{2} \right)$ has a fractional coordinate but since x and y are numbers of toys, hence they cannot be fractional. Thus, we will not check this point for Z. Now, from (i), (ii), and (iii) we get that the maximum value of Z is 1500 which we obtain at (12,15). Thus, we can say that: Maximum profit=1500 Number of types A toys=12 Number of type B toys=15 **Note:** While looking for solutions to the equations, we can take any values of x and y to find its corresponding value to obtain the solution. But we took x=0 once and then y=0 for the sake of convenience. Also, we have been given that it lies in the first quadrant by the inequalities $x\ge 0$ and $y\ge 0$ then by putting x=0 and y=0 we will also find the solution of these equations with these axes and we won’t need to find them again by solving them with the equations of the axes.