Question

A common emitter amplifier is designed with a n-p-n transistor.($\alpha =0.99$). The input impedance is $1k\Omega$ and load is $10k\Omega$. The voltage gain will be:
a) 9900
b) 99
c) 9.9
d) 990

Answer 1

In the above question a n-p-n transistor is used as a common emitter amplifier. Hence the voltage gain when connected across a a.c. is given by $\text{Voltage gain(}{{\text{A}}_{\text{V}}}\text{) = current gain(}\beta \text{) }\\!\\!\times\\!\\!\text{ resistance gain(}{{\text{A}}_{\text{R}}}\text{)}....\text{(1)}$.In the question the current gain of common base configuration is given to us, hence we can use the relation between $\text{ }\\!\\!\alpha\\!\\!\text{ and }\beta$ and then substitute for $\beta$ in the above equation to get the voltage gain in common emitter amplifier.

Complete answer:
To begin with let us first define the voltage gain, current gain and the resistance gain in a n-p-n transistor using a circuit diagram for common emitter amplifiers.

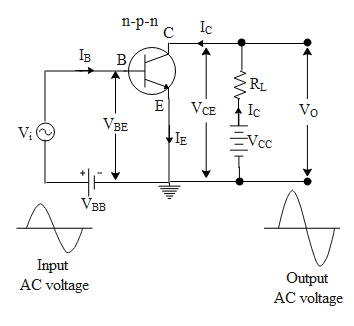
The voltage gain for a n-p-n transistor is defined as the small change in the output voltage($\Delta {{V}_{CE}}$) to a small change in the input voltage ($\Delta {{V}_{BE}}$) i.e. ${{A}_{V}}=\dfrac{\Delta {{V}_{CE}}}{\Delta {{V}_{BE}}}$.
The current gain in an common emitter configuration is defined as the ratio of small change in collector current($\Delta {{I}_{C}}$) to small change in base current ($\Delta {{I}_{B}}$) i.e. $\beta =\dfrac{\Delta {{I}_{C}}}{\Delta {{I}_{B}}}$
Resistance gain is defined as the ratio of Load resistance (${{R}_{L}}$ )to the impedance(${{R}_{I}}$ ) in an Ac circuit.
In the current gain for common base configuration is given to us i.e. $\alpha =0.99$. The relation between the current gain $\beta$ and $\alpha$ is given by,
$\beta =\dfrac{\alpha }{1-\alpha }$. Hence $\beta$ from the adjacent equation is numerically equal to,
$\begin{aligned} & \beta =\dfrac{\alpha }{1-\alpha } \\\ & \beta =\dfrac{0.99}{1-0.99}=\dfrac{0.99}{0.01}=99 \\\ \end{aligned}$
The resistance gain in the above circuit is numerically equal to,
${{R}_{GAIN}}=\dfrac{{{R}_{L}}}{{{R}_{I}}}=\dfrac{10\times {{10}^{3}}\Omega }{1\times {{10}^{3}}\Omega }=10$ . Hence substituting the current gain and the resistance gain in equation 1 we get,
$\begin{aligned} & \text{Voltage gain(}{{\text{A}}_{\text{V}}}\text{) = current gain(}\beta \text{) }\\!\\!\times\\!\\!\text{ resistance gain(}{{\text{A}}_{\text{R}}}\text{)} \\\ & \text{Voltage gain(}{{\text{A}}_{\text{V}}}\text{)}=99\times 10=990 \\\ \end{aligned}$

So, the correct answer is “Option D”.

Note:
The voltage gain is the ratio of the same physical quantity. Hence the quantity is dimensionless. It is also to be noted that the input and the output voltages are out of phase by an angle of 180 degrees. The basic aim of such transistor amplifiers is to increase the amplitude of the input voltages.