Question

A comes to rest after collision

Answer 1

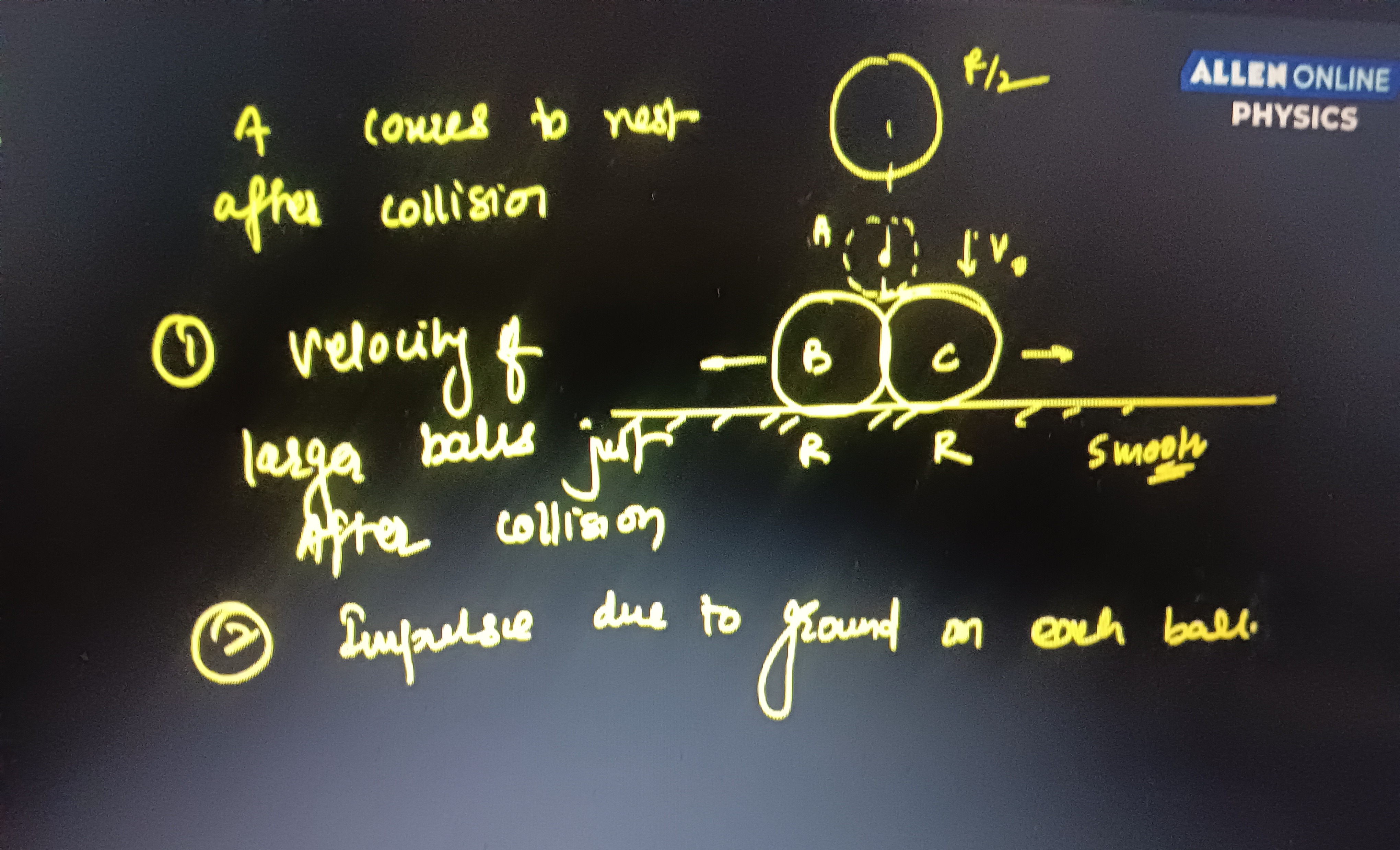
The velocity of the larger balls just after collision are: Ball B has zero velocity. Ball C has velocity $\frac{m_A}{m_B} \vec{v}_A$. The impulse due to the ground on each ball (B and C) is zero, assuming no vertical motion and instantaneous collision.

Answer 2

Let $m_A$ be the mass of ball A, and $m_B$ be the mass of balls B and C. Let $\vec{v}_A$ be the initial velocity of ball A. \textbf{Collision of A with B:} By conservation of linear momentum, $m_A \vec{v}_A = m_A \vec{v}_A' + m_B \vec{v}_B'$. Given that A comes to rest after collision, $\vec{v}_A' = 0$. So, $m_A \vec{v}_A = m_B \vec{v}_B'$, which gives the velocity of B after colliding with A as $\vec{v}_B' = \frac{m_A}{m_B} \vec{v}_A$.

\textbf{Collision of B with C:} Balls B and C are identical ($m_B = m_C$). For an elastic collision between two identical bodies where one is initially at rest (C is at rest), the first body (B) stops, and the second body (C) moves with the velocity the first body had before the collision. Therefore, after B collides with C: Velocity of B, $\vec{v}_B'' = 0$. Velocity of C, $\vec{v}_C' = \vec{v}_B' = \frac{m_A}{m_B} \vec{v}_A$.

The "larger balls" are B and C. After the entire sequence of collisions: Ball B comes to rest ($\vec{v}_B'' = 0$). Ball C moves with a velocity $\vec{v}_C' = \frac{m_A}{m_B} \vec{v}_A$.

\textbf{Impulse due to ground on each ball:} For balls B and C resting on a horizontal surface, their vertical momentum is zero. Assuming the collisions are horizontal and instantaneous, there is no change in their vertical momentum. Therefore, the net vertical impulse on balls B and C is zero. This means the impulse due to the ground on each of these balls is zero.