Question

A column of mercury of length h=10cm is contained in the middle of a narrow horizontal tube of length $1\;m$ closed at ends. The air in both halves of the tube is under a pressure of P = 76cm of mercury. The tube is now slowly made vertical. The distance moved by mercury will be:
A). 4.5 cm
B). 3.0 cm
C). 2.5 cm
D). 1.2 cm

Answer 1

First find the volume of the air columns when the tube is placed horizontally. Then, assuming the distance moved by the mercury when the tube is made vertical be x, determine the new volume of the air columns. Now, given that all of this occurs isothermally, we can assume that the product of the pressure and volume remains constant throughout. Use this to obtain expressions for the vertical pressure of the air columns.
Then, we know that the difference in these two pressures is due to the 10 cm of Hg between them. Equate the difference in pressure to this value and solve it arithmetically to arrive at a quadratic equation, whose positive solution will give the distance moved by the mercury upon the tube being made vertical.
Formula Used: Boyle’s law: $P_1V_1 = P_2V_2$

Complete step-by-step solution:
We are given that the length of the mercury column is $10\;cm = 0.1\;m$. The length of the whole tube $l = 1\;m$. The tube is placed horizontally, so the pressure experienced by the air in both halves is $P_0 = 76 = 0.76\;m \;of \;Hg$. The length of each half of the air column will be $l_0 = \dfrac{1-0.1}{2} = \dfrac{0.9}{2} = 0.45\;m$

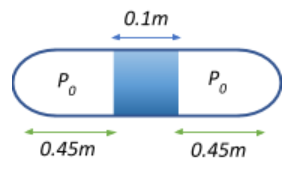
Thus, the volume of each half of the air column at the two sides of the tube will be $V_0 = 0.45 \times A$, where A is the cross-sectional area of the tube.
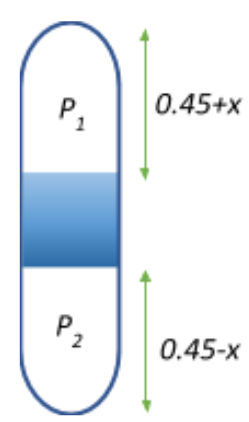
Now, when the tube is flipped to the vertical position, let the mercury be displaced by $x\;m$.
Then the volume of the upper part now becomes $V_1 = (0.45+x)A$, and
The volume of the lower part becomes $V_2 = (0.45-x)A$.
Let the new pressure of air at the upper part be $P_1$ and at the lower part be $P_2$

This change in the volume of air columns in the tube will correspondingly change the pressure, and this occurs as an isothermal process where the tube sees no change in the overall temperature.
This means that the product of the pressure and volume are observed to be constant. This is given by Boyle’s law: $PV = constant$
Applying Boyle’s law to the upper air column:
$P_0 V_0 = P_1 V_1 \Rightarrow 0.76 \times (0.45\times A) = P_1 \times ((0.45 +x) \times A)$
$\Rightarrow P_1 = \dfrac{0.76 \times 0.45}{(0.45 + x)}$
Similarly, applying Boyle’s law to the lower air column:
$P_0V_0 = P_2 V_2 \Rightarrow 0.76 \times (0.45\times A) = P_2 \times ((0.45 -x) \times A)$
$\Rightarrow P_2 = \dfrac{0.76 \times 0.45}{(0.45 - x)}$
Now, we know that $P_2$>$P_1$ and the difference in pressure between the upper and lower parts of the tube will be due to the mercury column of length $0.1\;m$ between them.
$\Rightarrow P_2 – P_1=0.1$
$\Rightarrow \dfrac{0.76 \times 0.45}{(0.45 - x)} - \dfrac{0.76 \times 0.45}{(0.45 + x)} = 0.1$
$\Rightarrow \dfrac{(0.76 \times 0.45 \times (0.45+x)) – (0.76 \times 0.45 \times (0.45-x))}{(0.45+x)(0.45-x)} = 0.1$
$\Rightarrow \dfrac{0.342(0.45 + x – 0.45 +x)}{0.45^2-x^2} = 0.1$
$\Rightarrow \dfrac{0.342 \times 2x}{0.2025-x^2} = 0.1$
$\Rightarrow 0.684x = 0.1(0.2025-x^2)$
Dividing the whole equation by 0.1
$\Rightarrow 6.84 x = 0.2025 -x^2 \Rightarrow x^2 + 6.84 – 0.2025 = 0$
Solving this quadratically:
$x = \dfrac{-b \pm \sqrt{b^2-4ac}}{2a}$, taking a = 1, b = 6.84 and c = -0.2025:
$\Rightarrow x = \dfrac{-6.84 \pm \sqrt{(6.84)^2-(4 \times 1 \times -0.2025)}}{2\times 1} = \dfrac{-6.84 \pm 6.89}{2}$
Taking only the positive value: $x = \dfrac{-6.84 +6.89}{2} = 0.0295\;m = 2.95\;cm \approx 3\;cm$
We get that the mercury is displaced by approximately 3 cm.
Therefore, the correct option is B. 3.0 cm

Note: Remember that Boyle’s law is an empirical relation that was formulated on the basis of the behavior of a gas of a given mass which was subjected to an exertion of pressure while maintaining a constant temperature. From this law, we can infer that changing the pressure exerted on the gas by some factor would inevitably change the volume of the gas by the same factor such that the product of the two remains the same, irrespective of any changes specific to just pressure or volume. Also, do not forget that Boyle’s law is an ideal gas law. Real gases, however, exhibit deviations from this law.