Question

A coin is placed on a rotating turntable. It gets just slipped when it is placed at a distance of 16cm from the center. If the angular velocity of the turntable was doubled, it would just slip at a distance (in cm) of
A. 2cm
B. 3cm
C. 4cm
D. 5cm

Answer 1

Remember that the force that provides the centripetal force to the coin to remain in its circular motion is that of static friction. The coin gets just flipped when it overcomes this force. By equating these two forces, we realize that the square of angular velocity times the distance of the coin from the centre is a constant. With that you could find the required distance.

Formula used:
Expression for force of static friction,
${{F}_{S}}=\mu mg$
Expression for centripetal force,
${{F}_{c}}=m{{\omega }^{2}}r$

Complete step by step answer:
We are given a turntable with angular velocity ω and a coin is kept at a distance r from the centre. In such a condition, the force that keeps the coin in circular motion is the centripetal force$({{F}_{S}})$ . And this force is provided by the static frictional force$\left( {{F}_{S}} \right)$ . That is,
${{F}_{C}}={{F}_{S}}$ ……………………. (1)

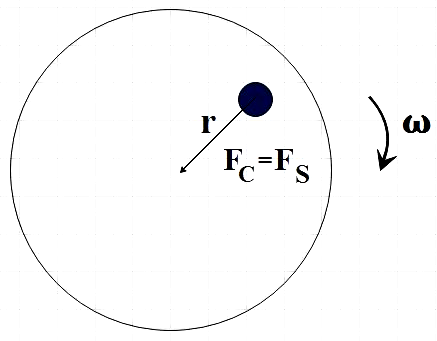
Also, we have the expressions for the centripetal as well as static frictional force.
Centripetal force that keeps any object in its circular motion and is given by,
${{F}_{c}}=\dfrac{m{{v}^{2}}}{r}$
In the terms of angular velocity ω, centripetal force is given by,
${{F}_{c}}=m{{\omega }^{2}}r$ …………………… (2)
Where, $\omega =\dfrac{v}{r}$
Static frictional force can be expressed as,
${{F}_{S}}=\mu N$
Where, N is the normal force acting on the body. N=mg in this case, so,
${{F}_{S}}=\mu mg$ ……………….. (3)
Substituting (2) and (3) in equation (1) we get,
$m{{\omega }^{2}}r=\mu mg$
$\Rightarrow {{\omega }^{2}}r=\mu g$ ………………. (4)
Since, μ and g remain constant throughout the given motion, ${{\omega }^{2}}r$also becomes constant.
Coin is said to be at the verge of slipping when it is about to overcome the force of static friction.
We are given that, for ω angular velocity of the turntable that coin should be at r=16cm to just flip.
We are supposed to find the distance (r’) at which the coin should be kept to just flip when the angular velocity of the turntable is doubled.
We know, ${{\omega }^{2}}r$= constant, therefore,
${{\omega }^{2}}r={{\left( \omega ' \right)}^{2}}r'$
But ω’=2ω, so,
${{\omega }^{2}}r={{\left( 2\omega \right)}^{2}}r'$
$r=4r'$
$r'=\dfrac{r}{4}=\dfrac{16}{4}=4cm$
So, when angular velocity is doubled, the coin should be kept at a distance of 4cm to get just flipped.
Hence, the solution to this question is, option C.

Note:
Don’t confuse centripetal force with centrifugal force. Centripetal force is the force that is directed towards the center of curvature and keeps you in a circular motion around that curvature. While, we call centrifugal force the one that tends to throw you off from that circular motion (remember your experience on a merry-go-round). But it is only the inertia of your body that we call centrifugal force as there is no known force in earth’s frame of reference that throws you off!