Solveeit Logo
Login

Question

Question: A coil of self inductance 10mH and resistance \(0.1\Omega \) is connected through a switch to a batt...

A coil of self inductance 10mH and resistance 0.1Ω0.1\Omega is connected through a switch to a battery of internal resistance 0.9Ω0.9\Omega . After the switch is closed the time taken for the current to attain 80% of saturation value is: (take ln5=1.6)
a)0.103s
b)0.106s
c)0.002s
d)0.324s

Explanation

Solution

The internal resistance of the cell always adds the net resistance in the circuit. Hence it can be put in series with the other components. To solve the above question first we need to obtain the expression for current in LR circuit and accordingly we can determine the time at which the current to attains 80% of saturation value

Complete answer:
The value of internal resistance can be put in series in the circuit with other components. Hence the net resistance in the circuit will be 1Ω1\Omega .

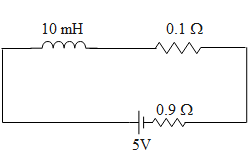
Using the Kirchhoff’s voltage law for the above circuit we get,
V=VL+VRV={{V}_{L}}+{{V}_{R}} , where ‘V’ is the applied emf, VL{{V}_{L}} is the voltage across the inductor and VR{{V}_{R}} is the voltage across the resistor. The instantaneous voltage across the resistor is VR=iR{{V}_{R}}=iR (‘i’ is the current in the circuit and R is the resistance in the circuit) and the instantaneous voltage across the inductor is VL=Ldidt{{V}_{L}}=L\dfrac{di}{dt} (L is the inductance in the circuit and didt\dfrac{di}{dt} is the rate of change of current in the circuit).
Substituting this in equation of Kirchhoff’s law we get,
V=VL+VR ⇒V=Ldidt+iR \begin{aligned} & V={{V}_{L}}+{{V}_{R}} \\\ & \Rightarrow V=L\dfrac{di}{dt}+iR \\\ \end{aligned}
Solving the above differential equation,
didt=VL−iRL.....(1) ⇒−R(1V−iR)di=−RLdt ⇒log⁡(V−iR)=−RLt+C ⇒V−iR=ke−RLt \begin{aligned} & \dfrac{di}{dt}=\dfrac{V}{L}-\dfrac{iR}{L}.....(1) \\\ & \Rightarrow -R\left( \dfrac{1}{V-iR} \right)di=-\dfrac{R}{L}dt \\\ & \Rightarrow \log (V-iR)=-\dfrac{R}{L}t+C \\\ & \Rightarrow V-iR=k{{e}^{-\dfrac{R}{L}t}} \\\ \end{aligned}
At time t=0, the current in the circuit is zero. Therefore
V−(0)R=ke−RL(0) ⇒V=k \begin{aligned} & V-(0)R=k{{e}^{-\dfrac{R}{L}(0)}} \\\ & \Rightarrow V=k \\\ \end{aligned}
Substituting this in equation 1 we get,
V−iR=Ve−RLt iR=V−Ve−RLt ⇒i=VR(1−e−RLt),∵VR=iMax→Ohms law ⇒i=iMax(1−e−RLt) \begin{aligned} & V-iR=V{{e}^{-\dfrac{R}{L}t}} \\\ & iR=V-V{{e}^{-\dfrac{R}{L}t}} \\\ & \Rightarrow i=\dfrac{V}{R}\left( 1-{{e}^{-\dfrac{R}{L}t}} \right),\because \dfrac{V}{R}={{i}_{Max}}\to Ohms\text{ }law \\\ & \Rightarrow i={{i}_{Max}}\left( 1-{{e}^{-\dfrac{R}{L}t}} \right) \\\ \end{aligned}
So when the current in the circuit reaches 80% of saturation value i.e. imax⁡{{i}_{\max }} the time taken ‘t’ is,
i=iMax(1−e−RLt) ⇒0.8iMax=iMax(1−e−1Ω10mHt) ⇒0.8−1=−e−110×10−3t ⇒0.2=e−110×10−3t \begin{aligned} & i={{i}_{Max}}\left( 1-{{e}^{-\dfrac{R}{L}t}} \right) \\\ & \Rightarrow 0.8{{i}_{Max}}={{i}_{Max}}\left( 1-{{e}^{-\dfrac{1\Omega }{10mH}t}} \right) \\\ & \Rightarrow 0.8-1=-{{e}^{-\dfrac{1}{10\times {{10}^{-3}}}t}} \\\ & \Rightarrow 0.2={{e}^{-\dfrac{1}{10\times {{10}^{-3}}}t}} \\\ \end{aligned}
Since 0.2 is equal to 1/5
⇒ln⁡15=−110×10−3t ⇒−ln⁡5=−110×10−3t ⇒1.6=110×10−3t ⇒t=0.016s \begin{aligned} & \Rightarrow \ln \dfrac{1}{5}=-\dfrac{1}{10\times {{10}^{-3}}}t \\\ & \Rightarrow -\ln 5=-\dfrac{1}{10\times {{10}^{-3}}}t \\\ & \Rightarrow 1.6=\dfrac{1}{10\times {{10}^{-3}}}t \\\ & \Rightarrow t=0.016s \\\ \end{aligned}

Hence the correct answer of the above question is option b.

Note:
The value of current in the LR circuit is an exponential function of time. After infinite time the current in the circuit will be maximum. It is during this time the inductor does not play any role in the circuit in a d.c supply.